43. Многомерные непрерывные случайные величины

Система из m одномерных непрерывных случайных величин, у которой пространством элементарных событий является m-мерное арифметическое пространство либо его область, имеющая ненулевой объем.

M-мерная плотность вероятности удовлетворяет выражению

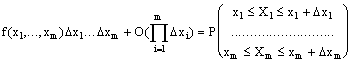
M-мерной функцией распределения называется числовая скалярная функция m действительных аргументов, которая численно равна:

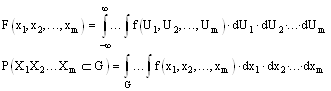
Случайные величины x1, x2, ... xm независимы, если

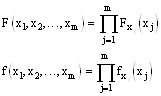
Доказать, что если m-мерная случайная величина порождена композицией m-мерных испытаний, то события независимы.

Запишем аналог формул

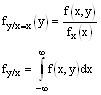
Для многомерного случая.

Для получения плотности вероятности необходимо n-мерную плотность проинтегрировать в бесконечных пределах по переменным, которые соответствуют случайным величинам, не входящим в

Найдем плотность n-мерной случайной величины.

< Предыдущая		Следующая >