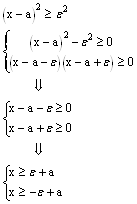34. Неравенство Чебышева

Рассмотрим случайную величину X с конечным мат. ожиданием и дисперсией

Для любого неотрицательного числа t вероятность наступления события

Пусть Z - непрерывная случайная величина с плотностью вероятности f(Z). Пространство событий величины Z (0; ¥). Тогда имеет место неравенство

Доказать неравенства

Рассмотрим два сложных события

A - произвольное действительное число.

Показать самим, что x - удовлетворяет и одному и другому неравенству.

Тогда справедливо

В данном случае

Равномерность неравенств при e>0

Или, в частности, при a=n=MX

При e=st справедливо неравенство Чебышева.

< Предыдущая		Следующая >