28. Непрерывные случайные величины

Будем рассматривать пространство элементарных событий как совокупность всех точек числовой оси. В этом случае введенная ранее функция распределения имеет вид: .

Пусть функция распределения является непрерывной. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a, где a - произвольное действительное число.

P(X=a).

Рассмотрим неравенство:

Доказать самим.

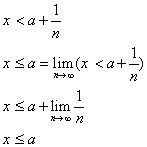
Следовательно:

Мы впервые столкнулись с ситуацией, когда событие принципиально может произойти в результате испытания, но имеет вероятность равную 0 . В инженерном толковании это означает: в данной конечной серии испытаний данное событие никогда не произойдет.

Случайная величина X называется Непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.

P(a£X<b)=P(a£X£b)=F(b)-F(a)

Если от сложного события вычесть конечное либо счетное множество, вероятность наступления нового события останется неизменной.

Функция f(x) - числовая скалярная функция действительного аргумента x называется Плотностью вероятности, и существует в точке x, если в этой точке существует предел:

< Предыдущая		Следующая >