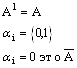19. Биномиальное распределение

N испытаний называются Системой испытаний Бернулли, если испытания независимы, в каждом из них происходит событие , либо с вероятностью наступления P(A) = p;

Найдем вероятность того, что в результате проведенных n испытаний событие А произошло m раз:

Рассмотрим композицию n независимых испытаний и построим композиционное пространство элементарных событий.

Общий вид элемента этого пространства следующий:

Где

При этом вероятность наступления такого события равна:

(умножение при независимых событиях)

Найдем вероятность наступления любого элементарного события из композиционного пространства:

Рассмотрим в композиционном вероятностном пространстве событие: в n испытаниях событие A произошло m раз.

Событие A состоит из - общее кол-во элементарных событий, в которое входит событие А. А произошло m раз, - n-m раз. Вероятность каждого из этих элементарных событий одинакова и равна:

Следовательно, на основании III аксиомы теории вероятности результат равняется:

(сложение вероятностей)

< Предыдущая		Следующая >