09. Классическое определение вероятности

Пусть W состоит из конечного числа элементарных событий и все элементарные события равновероятны, т. е. ни одному из них из них нельзя отдать предпочтения до испытания, следовательно, их можно считать равновероятными.

Тогда достоверное событие m - количество равновероятных событий

, ,

Пусть произвольное событие Тогда 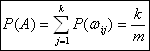, т. е. событие A состоит из k элементарных событий.

Если элементарные события являются равноправными, а, следовательно, и равновероятными, то вероятность наступления произвольного события равна дроби числитель которой равен числу элементарных событий, входящих в данное, а знаменатель - общее число элементарных событий.

< Предыдущая		Следующая >