2.5. Минимальное остовное дерево

Найти минимальное остовное дерево в неориентированном нагруженном графе.

Алгоритм выделения минимального остовного дерева в неориентированном нагруженном графе G

1) Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G2 графа G. Положим I:=2.

2) Если I=N(G), то задача решена и Gi – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).

3) Строим граф Gi+1. Для этого добавим к графу Gi новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа Gi и одновременно вершине, не содержащейся в Gi. Вместе с этим ребром включаем в Gi+1 и эту инцидентную ему вершину. Присваиваем I:=I+1 и переходим к шагу 2).

Пример.

Найдем минимальное остовное дерево в неориентированном нагруженном графе, изображенном на рис.14.

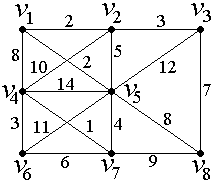
Рис.14.

Обозначим ребро, соединяющее вершины Vi и Vj через Xij.

Для удобства использования приведенного выше алгоритма решения поставленной задачи, составим матрицу длин ребер. В рассматриваемом графе количество вершин N=8, следовательно, матрица длин ребер графа G Будет иметь размерность 8×8 и выглядеть следующим образом:

Согласно приведенному выше алгоритму, выбираем ребро минимальной длины (выбираем среди элементов матрицы C(G), минимальное − это C47=1) и вместе с инцидентными ему двумя вершинами относим к графу G2. Таким образом, . Длина дерева G2 будет равна L(G2)=C47=1. Поскольку , продолжаем работу алгоритма. По четвертой и седьмой строкам ищем минимальное число (за исключением использованной единицы) − ребро минимальной длины, инцидентное либо вершине V4, либо V7. Выбираем ребро X46 с длиной C46=3 и вместе с вершиной V6 добавляем к графу G2, обозначая его теперь как G3: , при этом L(G3)=C47+C46=1+3=4. Аналогично находим графы:

, ;

,;

,

;

,

;

,

.

Поскольку I=8=N(G), работа алгоритма заканчивается.

Таким образом, искомое минимальное остовное дерево графа G − граф G8, изображенный на рис. 15, длина которого равна 22.

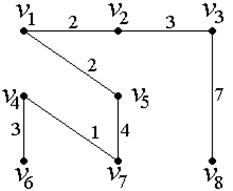
Рис.15.

< Предыдущая		Следующая >