1.8. Нагруженные графы
Нагруженный граф − ориентированный граф D=(V,X), на множестве дуг которого определена некоторая функция ![]() , которую называют весовой функцией.
, которую называют весовой функцией.
Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).
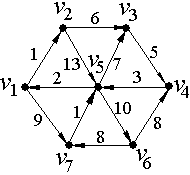
Рис. 5.
Обозначения: для любого пути П нагруженного ориентированного графа D через L(П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П).
Величина L называется Длиной пути.
Если выбрать веса равными 1, то придем к ненагруженному графу.
Путь в нагруженном ориентированном графе из вершины V в вершину W, где V¹W, называется Минимальным, если он имеет наименьшую длину.
Аналогично определяется Минимальный путь в нагруженном графе.
Введем матрицу длин дуг C(D)=[Cij] порядка N, причем

Свойства Минимальных путей в нагруженном ориентированном графе
1) Если для " дуги ![]()
![]() , то " минимальный путь (маршрут) является простой цепью;
, то " минимальный путь (маршрут) является простой цепью;
2) если ![]() минимальный путь (маршрут) то для " I,J :
минимальный путь (маршрут) то для " I,J : ![]() путь (маршрут)
путь (маршрут) ![]() тоже является минимальным;
тоже является минимальным;
3) если ![]() − минимальный путь (маршрут) среди путей (маршрутов) из V в W, содержащих не более K+1 дуг (ребер), то
− минимальный путь (маршрут) среди путей (маршрутов) из V в W, содержащих не более K+1 дуг (ребер), то ![]() − минимальный путь (маршрут) из V в U среди путей (маршрутов), содержащих не более K дуг (ребер).
− минимальный путь (маршрут) из V в U среди путей (маршрутов), содержащих не более K дуг (ребер).
| < Предыдущая | Следующая > |
|---|