1.5. Матрицы достижимости и связности

Пусть A(D) – матрица смежности ориентированного псевдографа D=(V,X) (или псевдографа G=(V,X)), где V={V1,…, VN}. Обозначим через Ak=[A(K)Ij] K-ю степень матрицы смежности A(D).

Элемент A(K)Ij матрицы Ak ориентированного псевдографа D=(V,X) (псевдографа G=(V,X)) равен числу всех путей (маршрутов) длины K из Vi в Vj.

Матрица достижимости ориентированного графа D − квадратная матрица T(D)=[Tij] порядка N, элементы которой равны

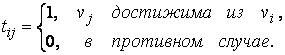
Матрица сильной связности ориентированного графа D − квадратная матрица S(D)=[Sij] порядка N, элементы которой равны

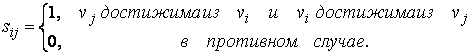
Матрица связности графа G − квадратная матрица S(G)=[Sij] порядка N, элементы которой равны

Утверждение 3. Пусть D=(V,X) – ориентированный граф, V={V1,…, VN}, A(D) – его матрица смежности. Тогда

1) T(D)=sign[E+A+A2+A3+… AN-1],

2) S(D)=T(D)&TT(D) (TT-транспонированная матрица, &- поэлементное умножение).

Пусть G=(V,X) – граф, V={V1,…, VN}, A(G) – его матрица смежности. Тогда

S(G)=sign[E+A+A2+A3+… AN-1] (E- единичная матрица порядка N).

< Предыдущая		Следующая >