14. Сети и потоки в сетях. Стационарные потоки. Алгоритм Форда-Фалкерсона поиска максимального стационарного потока

Пусть - некоторый орграф и вещественно-значная функция на множестве ребер; тогда пара называется Сетью, а функция в контексте сети называ-ется Функцией пропускной способности или Пропускной способностью сети.

Всякая функция , удовлетворяющая неравенству , называется Пото-ком в сети. В обсуждении свойств потоков в сети традиционно используется следующее обо-значение:

Пусть - любая функция и - два любых подмножества вершин; символ будет обозначать сумму значений функции на ребрах таких, что и ; если состоит из единственной вершины , то символ обозначает сумму весов ребер, начинающихся в и заканчивающихся в вершинах из ; аналогичный смысл имеет символ - сумма значений функции на ребрах, начинающихся в и заканчивающихся в вершине .

Поток в сети называется Стационарным, если существуют две вершины и число такие, что выполнены следующие условия:

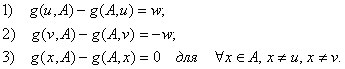
В этой ситуации число Называется Величиной потока , вершина называется Источни-

Ком, а вершина - Стоком потока .

Известна следующая классическая Задача о максимальном потоке: в данной сети для данного источника и для данного стока найти стационарный поток максимально возможной величины. Можно доказать, что такая задача всегда имеет решение. Один из способов ее ре - шения называется Алгоритмом Форда-Фалкерсона. Сформулируем этот алгоритм по шагам.

Шаг 0. Фиксируем на данной сети с источником и стоком произвольный стационарный поток , например - поток, тождественно равный нулю (т. е. равный нулю на каждом ребре данного орграфа ). Нетрудно проверить, что такой поток действитель-но стационарный и имеет величину 0.

Шаг 1. Около вершины поставим пометку следующего вида:

.

Здесь символ обозначает число, заведомо превосходящее все числа, которые будут участ-вовать в дальнейших рассмотрениях (в случае программирования это - компьютерная беско-нечность, т. е. самое большое число, допускаемое данным программным средст-вом).

Замечание. Почти все дальнейшие действия по алгоритму представляют собой расста-новку пометок около некоторых вершин. Цель этой расстановки в том, чтобы в конце концов поставить пометку у стока или установить, что сток пометить невозможно. В первом

Случае окажется возможным заменить имеющийся стационарный поток на другой стацио-нарный поток, имеющий величину, большую, чем величина потока . После этого надо будет запустить все сначала. Во втором случае окажется, что имеющийся поток оптимален, т. е. его величина имеет максимальное возможное значение. Каждая пометка, кроме уже проставленной около источника , будет иметь вид , где - некоторое число, а - имя одной из вер-шин орграфа , причем реально в пометке это имя будет либо в виде , либо в виде .

Шаг 2. Пусть - некоторое ребро, начало которого, т. е. вершина , уже имеет некоторую пометку (или, если - это источник , то пометку , где ). Если , т. е. поток равен на ребере пропускной способности , то пометка у вершины Не проставляется. Если же , то пометка у вершины выставляется следующим образом.

На первом месте в пометке будет стоять символ , т. е. пометка будет такой: , где число Еще нужно найти. Положим

.

Пусть теперь такое ребро, у которого пометку имеет конец, т. е. вершина имеет пометку . Если , то пометку у вершины не выставляют; если же , то вершина получает пометку , где

.

Процедура расстановки пометок в соответствии с Шагом 2 проводится до тех пор, пока не окажется помеченной вершина , или до тех пор, пока не выяснится, что вершину поме-тить невозможно. Можно доказать, что в последнем случае поток , с помощью которого проводился весь Шаг 2, Имеет максимальную возможную величину, и задача решена.

Если же вершина оказалась помеченной, то переходим к следующему шагу. Отметим принципиальную подробность: если вершина оказалась помеченной, то Число, фигурирующее в пометке, обязательно положительно.

Шаг 3. Пусть вершина имеет пометку . Мы изменим сейчас поток на не-скольких ребрах данного графа, в результате чего получится новый стационарный поток из источника в сток , величина которого будет на (это число указано в пометке стока ) больше величины потока .

Если вершина имеет пометку , то на ребре изменим поток , прибавив к его значению на этом ребре число . Если вершина имеет пометку , то на ребре изменим поток , вычитая из его значения на этом ребре число .

Затем перейдем к вершине и проделаем то же, что только что делалось относительно вершины ; при этом прибавлять или вычитать будем прежнее число . Продолжая так, в со-ответствии с пометками, отбирать ребра графа и менять на них значение потока (на каждом от-бираемом ребре - на одно и то же число !), мы придем к источнику . Это будет означать завершение изменения потока. Можно доказать, что Полученный в результате поток является стационарным и его величина на больше величины исходного потока .

Затем нужно повторить все сначала с уже новым базовым стационарным потоком.

Пример. Найти максимальный стационарный поток из в в следующей сети (числа у стрелок означают пропускную способность):

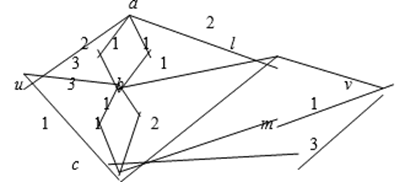
Считаем, что исходный стационарный поток тождественно равен нулю. Проставляем пометку около вершины : она такова - . Выбираем далее для пометки вершину ; соответст-вующая пометка: . Выбираем далее для пометки вершину ; соответствующая пометка: . Теперь появилась возможность пометить и вершину ; соответствующая пометка : .

Возникла возможность поток увеличить на 1. Для этого на ребре положим его рав-ным 1 (а не нулю, как это было для исходного потока), также равным 1 новый поток будет и на ребрах и . На остальных ребрах поток остается равным нулю.

Новый поток имеет величину 1, он стационарен с источником и стоком . Повторим теперь процедуру сначала, стремясь поставить пометку к стоку .

Вершину пометим пометкой . Далее пометим вершину ; соответствующая пометка: . Далее пометим вершину ; соответствующая пометка: . Теперь поме-тим вершину ; соответствующая пометка: . Теперь снова увеличим на 1 значения по-тока на ребрах . Новый поток будет тоже стационарен, но уже величины 2.

Вновь поставим пометку у вершины и попытаемся увеличить имеющийся стационарный поток величины 2.

Пометим вершину ; соответствующая пометка: . Далее пометим вершину ; соответствующая пометка: . Далее поме-тим вершину ; соответствующая пометка: . Вновь изменим поток на 1: прибавим 1 к значениям прежнего потока на ребрах ,

. Вновь полученный поток имеет величину 3.

Дальнейшие попытки достигнуть пометками вершину не имеют успеха. Следова-тельно, максимальный стационарный поток найден.

< Предыдущая		Следующая >