03. Путь в графе и связные компоненты графа. Цепи, простые цепи, циклы, простые циклы. Операции удаления вершины, удаления ребра, подразбиения ребра. Дерево и его особенности
Пусть ![]() - граф и, как обычно,
- граф и, как обычно, ![]() .
.
Путь в графе - это символ вида
![]() ,
,
Где ![]() . Таким образом, среди вершин
. Таким образом, среди вершин ![]() и ребер
и ребер ![]() могут быть повторы. По символу пути на графической интерпретации графа можно воспроизвести «движение» от вершине к вершине, выбирая каждый раз очередное ребро в соот-ветствии с указанием в пути.
могут быть повторы. По символу пути на графической интерпретации графа можно воспроизвести «движение» от вершине к вершине, выбирая каждый раз очередное ребро в соот-ветствии с указанием в пути.
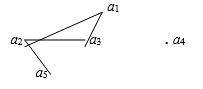
Вершины ![]() в приведенных выше обозначениях называются Концами пути и Связан-ными или Соединенными Путем L. Отдельным термином выделяют тот факт, что две вершины графа могут быть связаны некоторым путем: их называют Связанными. Например, в графе
в приведенных выше обозначениях называются Концами пути и Связан-ными или Соединенными Путем L. Отдельным термином выделяют тот факт, что две вершины графа могут быть связаны некоторым путем: их называют Связанными. Например, в графе
![]()
![]()
Вершины A3 и A5 связаны (путем ![]() ), а вершины A4 и A1 нет.
), а вершины A4 и A1 нет.
Граф, в котором связанны любые две вершины, называется Связным. Таким образом, выше приведен пример графа несвязного. Связной компонентой графа называется такой его подграф, который является сам по себе графом связным и при этом совпадающим с любым другим содержащим его связным подграфом. Таким образом, связный граф обладает единст-венной связной компонентой - это он сам. А вот приер графа с тремя связными компонетами (имена вершин не имеют значения):
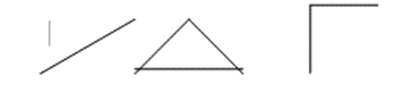
Путь без повторяющихся ребер называется Цепью, а цепь без повторяющихся вершин называется Простой. Цепь, в которой сопадают концевые вершины, называется Циклом, а цикл в котором нет повторяющихся вершин, кроме концевых, называется Простым.
Вот схематическое изображение простого цикла:

А вот схематическое изображение цикла, не являющегося простым:
Ведем теперь три стандартные операции над графами.
Удаление вершины. Пусть ![]() - граф и
- граф и ![]() . Удалить вершину A из графа G - это значит построить новый граф
. Удалить вершину A из графа G - это значит построить новый граф ![]() , в котором
, в котором ![]() и
и ![]() получается из B удалением всех ребер, инцидентных вершине A. Вот иллюстрация удаления вершины A из
получается из B удалением всех ребер, инцидентных вершине A. Вот иллюстрация удаления вершины A из
Графа:

Удаление ребра. Пусть ![]() - граф и
- граф и ![]() . Удалить ребро B - это значит построить новый граф
. Удалить ребро B - это значит построить новый граф ![]() , в котором
, в котором ![]() и
и ![]() . Вот иллюстрация удаления ребра графа:
. Вот иллюстрация удаления ребра графа:

Подразбиение ребра. Пусть ![]() - граф и
- граф и ![]() . Выполнить подразбие-ние ребра B - это значит построить новый граф
. Выполнить подразбие-ние ребра B - это значит построить новый граф ![]() , в котором
, в котором ![]() (т. е. Z - некая новая вершина) и
(т. е. Z - некая новая вершина) и ![]() . С графической точки зрения эта опе-рация означает «внесение в ребро новой вершины». Вот графическая иллюстрация:
. С графической точки зрения эта опе-рация означает «внесение в ребро новой вершины». Вот графическая иллюстрация: 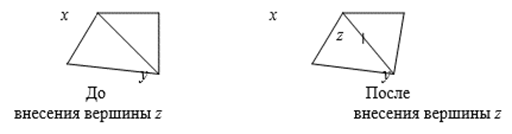 И в заключение введем один специальный вид графов. Деревом Называется связный граф без циклов. Вот пример дерева:
И в заключение введем один специальный вид графов. Деревом Называется связный граф без циклов. Вот пример дерева:
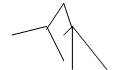
А вот пример графа, не являющегося деревом:
![]()
Если граф ![]() является деревом и число его вершин равно P, то о числе его ребер можно сказать совершенно определенно: кличество ребер равно
является деревом и число его вершин равно P, то о числе его ребер можно сказать совершенно определенно: кличество ребер равно ![]() . В каждом дереве имеется еще одна особенность: любые две вершины в дереве связаны и притом единственной простой цепью. Оба эти обстоятельства имеют несложные доказательства.
. В каждом дереве имеется еще одна особенность: любые две вершины в дереве связаны и притом единственной простой цепью. Оба эти обстоятельства имеют несложные доказательства.
| < Предыдущая | Следующая > |
|---|