49. Лемма Жордана

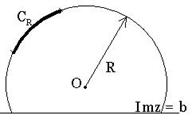
Лемма: Пусть задана горизонтальная прямая и дуга . Пусть такова, что непрерывна на и , тогда для .

 

 

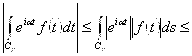
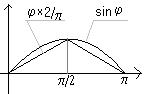
Доказательство: Не ограничивая общности, будем считать, что . Тогда . Известно, что . Покажем ограниченность . Пусть , тогда , . Нетрудно показать, что при выполняется неравенство (см. рисунок). Учитывая это и равенство , получаем :

Отсюда следует, что . Лемма доказана.

Замечание: Функция растет только в случае , что в условиях леммы невозможно за счет ограничения прямой .

< Предыдущая		Следующая >