100. Weighted Composited Price Indexes

At least two problems arise with the use of composite price indexes. The first concerns the arbitrary nature in which the units are expressed. Had Nipp and Tuck priced beef at $1.50 per half pound instead of $3.00 per pound, the price index would have been entirely different. Second, the composite indexes as computed do not take into account the fact that some goods sell in larger quantities than do other, less popular, products. No consideration is given to the respective amounts of each product that are sold.

For example, the composite index calculated for Nipp and Tuck gives the same importance, or weight, to beef as to pork, even though twice as much of the former may have been purchased by the consumers. In this case it’s better to compute a Weighted price index. Such a calculation assigns different weights to individual prices. These weights are established so as to measure the amounts sold of each product. This provides a more accurate reflection of the true cost of the consumer’s market basket of goods.

The quantities selected as weights can be taken from the number of units sold in (1) the base period or (2) the reference period.

Two common indexes are the Laspeyres index and the Paasche index. The Laspeyres index uses quantities sold in the base year as weights; the Paasche index relies on quantities sold in the reference year as weights. Each procedure has its own advantages and disadvantages.

The Laspeyres index uses Base period weights (quantities) in its calculation. The rationale is that these quantities will not change from one calculation to the next thereby permitting more meaningful comparisons over time.

To illustrate, consider the data for Nipp and Tuck in Table 9.3, which also includes the amounts sold for each product.

Table 9.3 – Nipp and Yuck, Inc.

The Laspeyres index is

(9.3)

Where PR is the price in the reference period, and PB and QB are the price and quantities sold in the period selected as the base period.

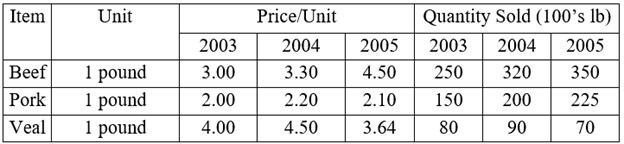
Table 9.4 shows computations necessary for the Laspeyres index using 2003 as the base year.

Table 9.4 – The Laspeyers Index for Nipp and Tuck (2003 = 100)

The numerator for L is figured by first multiplying each price by the quantities sold in the base period of 2003. The denominator is then determined by multiplying the price in the base year by the quantity in the base year. The index for 2003 is

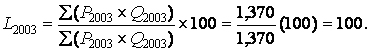
The index for 2004 uses the prices in the reference year (2004) and the quantities in the base year (2003) for the numerator:

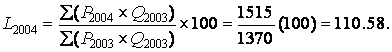
The numerator for 2005 uses prices in 2005 and quantities in 2003:

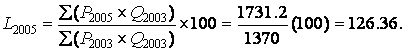
The interpretation of the Laspeyres index is like that for the earlier indexes. From 2003 to 2005, the price of the market basket for these three meat items increased by 26.36 percent. It would take $126.36 in 2005 to buy what $100 did in 2003. Or, alternatively, it would require $1.26 in 2005 to buy what $1.00 did in 2003.

Notice that The denominator is the same in all three years: the Laspeyres index always uses quantities from the base period.

The Paasche index, On the other hand, uses as weights the quantities sold in each of the various reference years. This has the advantage of basing the index on current consumer behavior patterns. As consumers change their buying habits, these changes in consumer tastes are reflected by the index. Commodities that no longer attract consumers’ interest, such as buggy whips and top hats, do not receive as much consideration. However, using of different quantity measures makes it impossible to attribute any differences in the index to changes in prices alone.

Thus, Paasche Index uses quantities sold in the reference period as the weight factor.

Its calculation is a bit more involved than the Laspeyres:

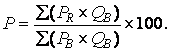(9.4)

The quantities for the reference years appear in both the numerator and denominator. Table 9.5 provides the computation necessary for the Paasche, using the Nippand Tuck data with 2003 as the base.

Table 9.5 – Paache Index for Nipp and Yuck (2003 = 100)

Item	P	Q	P	Q	P	Q
Beef	3.00	250	3.30	320	4.50	350
Pork	2.00	150	2.20	200	2.10	225
Veal	4.00	80	4.50	90	3.64	70
		750	1056	1575	960	1050
		300	440	472.5	400	450
		320	405	254.8	360	280
		1370	1901	2302.3	1720	1780

We must first multiply prices and quantities for all three years to get , which is used in the numerator. We also need the value for price in the base year, 2003, times the quantity for each reference year to get , which is used in the denominator. The Paasche index for 2003 is

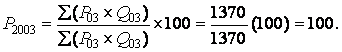
For 2004, it is

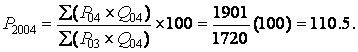
For 2005, it is

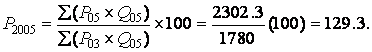
The usual interpretation applies.

The Laspeyres index requires quantity data for only one year and is easier to compute. Therefore, it is used more frequently than the Paasche. Since the base period quantities are always used, more meaningful comparisons over time are permitted.

However, the Laspeyres tends to overweigh goods whose prices increase. This occurs because the increase in price will decrease quantities sold, but the lower quantity will not be reflected by the Laspeyres index because it uses quantities from the base year. The Paasche, on the other hand, tends to overweigh goods whose prices go down. In an effort to offset these shortcomings. Fisher’s ideal index Is sometimes suggested. This index combines the Laspeyres and the Paasche by finding the square root of their product:

The interpretation of the Fisher index is subject to some dispute. For this reason, it is not widely used.

< Предыдущая		Следующая >