067. Sample Size for intervals of population proportion π
For the population proportion Z-value is found by using the following formula
Z = 
Where
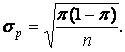
This can be rewritten to produce an expression for sample size.
N =  (6.8)
(6.8)
Where (P — π) is the difference between the sample proportion and the population proportion, and is therefore The error.
Formula (6.8) requires a value for π. However, π is the parameter we wish to estimate, and is unknown. This problem can be handled in one of two ways.
(1) A Pilot sample can be taken to obtain a preliminary value for π,
(2) π might be set as π = 0.5 for the purpose of determining sample size.
The second approach is often preferred because it is very “safe” or conservative – it will ensure the largest possible sample size given any desired level of confidence and error. This larger sample results from the fact that the numerator of Formula (6.10), which contains π(1 – π), will be maximized (thus, N will be maximized) if π = 1 – π= 0.5. There is no value other than 0.5 which you could assign to π that would make π(1 – π) larger. If π = 0.5, then π(1 – π) = 0.25. Any value other than 0.5 would result in π(1 – π) < 0.25. Thus, N would be smaller.
Example 6.7. Wally Simpleton is running for governor. He wants to estimate within 1 percentage point the proportion of people who will vote for him. He also wants to be 95 percent confident of his findings. How large should the sample size be?
N = 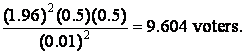
| < Предыдущая | Следующая > |
|---|