057. Тhe Principle of a Confidence Interval

A confidence interval has a Lower confidence limit (LCL) and an Upper confidence limit (UCL). These two limits are found by calculating а sample mean,, as a point estimate, adding a certain amount to it to get the UCL, and subtracting the same amount from it to get the LCL. The determination of that amount is the subject of this chapter.

The question may arise, “How can we construct an interval and then argue that we can be 95 percent confident that it contains if we don’t even know what the population mean is?” Recall from the discussion of the Empirical Rule that 95.5 percent of all sample means lie within two standard errors of the population mean. Then, of course, the population mean lies within two standard errors of 95.5 percent of all sample means. Therefore, starting with any sample mean, if we move two standard errors above that mean and two standard errors below that mean, we can be 95.5 percent confident that the resulting interval contains the unknown population mean. Figure 6.1 illustrates.

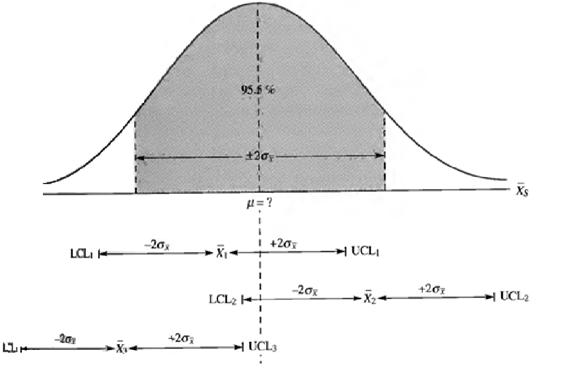
Figure 6.1 – Possible 95.5 Percent Confidence Interval for population mean

It should be noticed that if the sample yields 1, an interval extending two standard errors above and two standard errors below 1 does indeed include the value of the population mean. Similarly, if the sample had yielded a sample mean of 2, the resulting interval would also include the population mean. Remember, the discussion of sampling distributions showed that, from any population, we can get many different samples of some given size, each with its own mean. For the purpose of comparison, Figure 6.1 shows three of these possible sample means. Notice that only 3 lies so far from the population mean that an interval ±2 standard errors around either sample mean does not include the population mean. All other sample means will produce an interval that contains the population mean. The key to remember, then, is this: Since the population mean lies within two standard errors of 95.5 percent of all these sample means, then, given any sample mean, we can be 95.5 percent certain that the interval two standard errors around that sample mean contains the unknown population mean.

If we wish to construct the more conventional 95 percent interval (rather than the 95.5 percent discussed above), how many standard errors must we move above and below the sample mean? Since the Z-table contains only values for the area above or below the mean, we must divide the 95 percent by 2, yielding 47.50 percent, or 0.4750. We then find the Z-value corresponding to an area of 0.4750, which is Z = 1.96. Thus, to construct a 95 percent confidence interval, we simply specify an interval 1.96 standard errors above and below the sample mean. This value of 95 percent is called the Confidence coefficient.

In the case of medical research in which lives are at risk, or if our decisions have significant economic consequences, it may be desirable to calculate a higher level of confidence.

< Предыдущая		Следующая >