053. Using the Sample Distribution
Samples have a very direct and consequential impact on decisions that are made. An extremely common and quite useful application of a sampling distribution is to determine the probability that a sample mean will fall within a given range. Given that the sampling distribution will be normally distributed because (1) the sample is taken from a normal population or (2) N ≥ 30 and the Central Limit Theorem ensures normality in the sampling process.
There is a Conversion formula for determining the probability of selecting one observation that would fall within a given range
![]() ,
,
Where X is a single observation of interest; σ is the population standard deviation.
However, many business decisions depend on an entire sample – not just one observation. In this case, the conversion formula must be altered to account for the mean of several observations, ![]() . Therefore, when sampling is done, the conversion formula becomes
. Therefore, when sampling is done, the conversion formula becomes
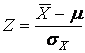 , (5.8)
, (5.8)
Where ![]() is the mean of several observations;
is the mean of several observations; ![]() is the standard error of the sampling distribution.
is the standard error of the sampling distribution.
Z – Formula has the Purpose: It is used to convert all normal distributions of ![]() to a standard form.
to a standard form.
Example 5.2. The Telcom recorded telephone messages for its customers. These messages averaged 150 seconds with a standard deviation of 15 seconds. Telcom wished to determine the probability that the mean duration of a sample of N = 35 phone calls is between 150 and 155 seconds, that is P(150 < ![]() < 155).
< 155).
Solution. Since N > 1 and a sample was taken, Formula (5.8) must be used. Then
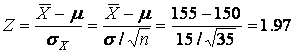 or an area of 0.4756.
or an area of 0.4756.
Thus, P(150 < ![]() < 155) = P(0 < Z< 1.97) = 0.4756. See it in Figure 5.3. so the probability that a sample of 35 calls will have duration within the range of 150 and 155 seconds is 47.56 percent. Such a quite big percentage is because the sampling distribution is less dispersed than the original population, i. e. the dispersion of original population is bigger than dispersion of the sampling distribution (
< 155) = P(0 < Z< 1.97) = 0.4756. See it in Figure 5.3. so the probability that a sample of 35 calls will have duration within the range of 150 and 155 seconds is 47.56 percent. Such a quite big percentage is because the sampling distribution is less dispersed than the original population, i. e. the dispersion of original population is bigger than dispersion of the sampling distribution (![]() >
> ![]() ).
).

Figure 5.3 – The Mean of a Sample Observations
By being able to predict the likelihood that a certain statistic will fall within a given range, decision making becomes more precise and scientific.
| < Предыдущая | Следующая > |
|---|