050. The Standard Error of the Sampling Distributions

The sampling distribution of the sample means also has a Variance. It measures the dispersion of the individual observations (sample means) around their mean (the grand mean). It can be found by

1. Determining the amount by which each of observations (sample means) differs from their mean (the grand mean).

2. Squaring those deviations.

3. Averaging the squared deviations by dividing by the number of sample means, K.

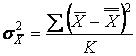. (5.2)

The Standard error of the sampling distribution,, can be found as

. (5.3)

This Standard error of the sampling distribution of sample means (or just Standard error) measures the dispersion of a set of a sample means around the grand mean. Thus, the Standard error is the measure of the variation of the sample means around the grand mean. As such, it measures the tendency to suffer sampling error in the effort to estimate the parameter.

A close approximation of the variance and standard error can be found much more easily with

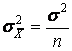. (5.4)

And , (5.5)

Where is the population variance.

The’s are less dispersed than original data. That is, , The standard error of the sampling distribution of the ’s, is Smaller than the standard deviation of the original population σ, i. e. . So, as the number of a sample observations N Increases, the spread in the sampling distribution, which is measured by the standard error, will Decrease. Therefore, there is less chance for a larger error.

The Finite population correction factor (FPC) must be used in calculating the standard error. The FPC is used only if n is more than 10 percent of N. If drawing is done without replacement from a finite population, the variance is

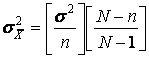. (5.6)

And the standard error becomes

, (5.7)

Where is the FPC. This expression accounts for the fact that N is finite, and thereby provides a more accurate statement of the variation in the sampling distribution.

< Предыдущая		Следующая >