042. The Binomial Distribution
A Binomial distribution based on the Bernoulli process and it must fit certain conditions:
1. There must be only two possible outcomes. One is identified as a success, the other as a failure.
2. The probability of success, π, remains constant from one trial to the next, as does probability of a failure, 1 – π.
3. The probability of a success in one trial is totally independent of any other trial.
4. The experiment can be repeated many times.
If the probability that any given trial will result in a success is known, it is possible to estimate how many successes there will be in a given number of trials.
 , (4.13)
, (4.13)
Where N is the number of trials; π is the probability of a success on any given trial; X is given number.
The Mean and Variance For Binomial distribution are calculated as
μ = Nπ and σ2 = Nπ(1 – π). (4.14)
It means that on average there are Nπ successes out of N trials.
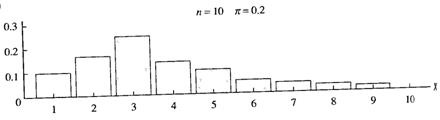
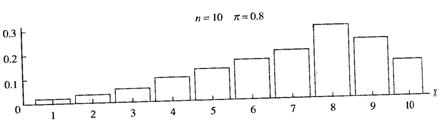
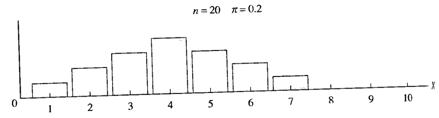
Figure 4.4 shows the Probability mass function (PMF), which assigns a probability to each value of X, for binomial distributions with different values of π and N.

A
B
C
D
Figure 4.3 – Probability Mass Functions: a – the distribution is symmetrical if π = 0.5; b – the distribution is skewed right if π < 0.5; c – the distribution is skewed left if π > 0.5; d – a distribution close to normality since N is bigger
| < Предыдущая | Следующая > |
|---|