034. Probability Approaches
The Relative frequency approach uses past data that have been empirically observed. It notes the frequency with which some event has occurred in the past and estimates the probability of its reoccurrence on the basis of these historic data. The probability of an event based on the relative frequency approach is determined by
![]() . (4.1)
. (4.1)
For Example, assume that during the last calendar year there were 50 births at a local hospital. Thirty-two of the little new arrivals were baby girls. The Relative frequency approach reveals that the probability that the next birth (or any randomly selected birth) is a female is determined as
![]() .
.
In many instances past data are not available. It is therefore not possible to calculate probability from previous performance. The only alternative is to estimate probability on the basis of our best judgment. The Subjective approach requires the assignment of the probability of some event on the basis of the best available evidence. The subjective approach is used when we want to assign probability to an event that has never occurred. For Example, the probability, that a woman will be elected president of the United States.
Of the three methods of assessing probability, the classical approach is one most often associated with gambling and games of chance. The classical probability of an event E is determined as
 . (4.2)
. (4.2)
Example 4.1. The probability of getting a head in the single flip of a coin is 1/2, i. e. using formula (4.2)
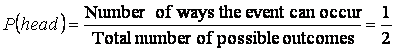 .
.
There is only one way that the event can occur (you get a head), and only two possible outcomes (a head or a tail).
Example 4.2. The probability of rolling a “3” with a six-sided die is
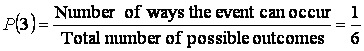 .
.
There is only one way that the event can occur (you roll a “3”), and six possible outcomes. Although the probability of rolling a “3” is 1/6, this is not suggest, that of every six rolls, one is a “3”. Instead, the implication is that if the die is rolled a large number of times (technically, an infinite number), one – sixth of the rolls produce a “3”.
Classical probability involves the determination of the probability of some event in an a priori manner (Before the fact). Thus, Before drawing a card from a deck of 52 cards, it can be determined that the probability of drawing an ace is
 .
.
| < Предыдущая | Следующая > |
|---|