030. The Normal Distribution and the Empirical Rule

The concept of a normal distribution is commonly encountered in statistical analysis and is of considerable importance. A Normal distribution is a distribution of continuous (not discrete) data that produces a bell-shaped, symmetrical curve like that shown in Figure 3.3.

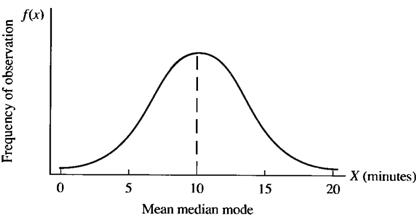
Figure 3.3 – A Normal Distribution

In a normal distribution, the Mean, median, and Mode are all Equal. Of importance, one-half of the observations are above the mean and one-half are below it. This means that one-half of the area under the curve is to the left of the mean, and one-half of the area under the curve is to the right of the mean.

The Empirical Rule tells that if include all normally distributed observations within one standard deviation of the mean (one standard deviation above the mean and one standard deviation below the mean) then 68.3 percent of all observations will be encompassed. Moving more than one standard deviation above and below the mean, a larger percentage of observations will be encompassed. The Empirical Rule specifies that

68.3 percent of the observations lie within plus or minus One standard deviation of the mean.

95.5 percent of the observations lie within plus or minus Two standard deviations of the mean.

99.7 percent of the observations lie within plus or minus Three standard deviations of the mean. Such observations are rarity and happen less that 1 percent of the time if the data are normally distributed.

The Empirical Rule also applies to Sample data. Thus, for example, produces a range that includes 95.5 percent of all observations in the sample. It is also important to remember that the Empirical Rule describes the total area under the normal curve that is found within a given range.

If the observations are highly dispersed, the bell-shaped curve will be flattened and spread out.

Example 3.12. There are a large number of observations for the time, in minutes, that it takes skiers to complete a particular run. The modal observation (μ = 10 in this case) is the one occurring with the greatest frequency and is therefore at the peak of the distribution. Given the skiers’ times, one standard deviation (σ = 2 minutes) above and below the mean of 10 yields a range of 8 to 12 minutes. Two standard deviations (σ = 4 minutes) yields a range of 6 to 14 minutes, and three standard deviations (σ = 6 minutes) – a range of 4 to 16 minutes. This is shown in Figure 3.4.

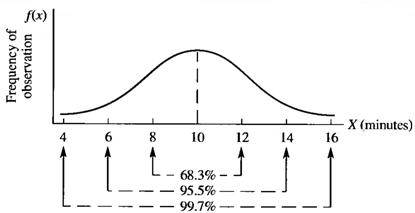
Figure 3.4 – Normally Distributed Times of 1,000 Skiers

According to the Empirical Rule, 997 of the 1,000 skiers took between 4 min and 16 min to complete the run. Thus, only 3 of the 1,000 skiers were either very good skiers and took less that 4 min or were lousy and took more than 16 min.

< Предыдущая		Следующая >