024. Measures of Dispersion for Ungrouped Data

In the efforts to describe a set of numbers, it has been seen that it is useful to locate the center of that data set. But identifying a measure of central tendency is not always sufficient. It often proves helpful if statisticians or managers can also cite the extent to which the individual observations are spread out around that center point.

Take the three small data sets shown here:

Data Set 1	Data Set 2	Data Set 3
0, 10	4, 6	5, 5

These data sets are not similar, but all three average exactly five. If not seeing the observations in each data set, and hearing only what the averages were, somebody might presume a similarity. To provide a more complete description of the data sets, a measure of how spread out the observations are from that mean of 5 is needed. A Measure of dispersion indicates to what degree the individual observations are dispersed or spread out around their mean.

Range

A simple, but not practically useful, measure of dispersion is the range. The Range is the difference between the highest observation and the lowest observation. Its advantage is that it is easy to calculate and gives at least some impression as to the makeup of the data set. Its disadvantage is that it takes only two of the, perhaps, hundreds of observations in the data set into consideration in its calculation. The rest of the observations are ignored.

Mean Absolute Deviation

It might seem that a practical approach to measuring the dispersion in a data set is to simply calculate the average amount by which the observations vary from the mean. This is called the Average deviation (AD). Formula (3.10) shows how the AD can be calculated.

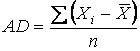. (3.10)

Example 3.7. Professor Willey Doezoff, a long-time resident of the statistics department, gave a quiz to his introductory statistics class last week. Eight of the brightest students scored 73, 82, 64, 61, 68, 52, and 73. The average is = 67, and is used to calculate the AD in the manner shown in Table 3.5.

Table 3.5 – Grades for Professor Doezoff’s Stat Class

73	73 – 67 = 6
82	82 – 67 = 15
64	64 – 67 = – 3
61	61 – 67 = – 6
63	63 – 67 = – 4
68	68 – 67 = 1
52	52 – 67 = – 15
73	73 – 67 = 6
Total	0 =

The result is an average deviation of 0. This happens because the pluses and minuses cancel each other out. The Average deviation (AD) of a data set is Always zero. A solution to this enigma is the Mean absolute deviation (MAD). MAD takes the absolute value of the differences, so the negatives do not cancel out the positives.

. (3.11)

Thus, for the example 3.7, MAD = 7. This value serves as an indication of the amount by which the individual observations are dispersed around their mean of 67: The higher the MAD the more the dispersion.

MAD is a “quick and dirty” method of measuring the amount of deviation in a data set.

< Предыдущая		Следующая >