022. Measures of Central Tendency for Grouped Data

If the data have been grouped into classes in a frequency table, it is impossible to determine measures of central tendency by the methods just discussed since the individual values are not given. Alternative approaches must be found. It should be kept in mind that computations made using grouped data are only approximations.

Mean

In calculating the mean from grouped data, the assumption is made that the observations in each class are equal to the class midpoint. Other words, the frequency and midpoint of each class must be taken into consideration when computing the mean using grouped data.

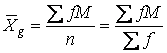, (3.7)

Where F is the frequency or number of observations in each class; M is the midpoint of each class; N is the sample size and equals the combined frequencies in all classes.

Example 3.6. The frequency table for Pigs&People Airlines was developed in Chapter 2 and repeated in Table 3.3.

Table 3.3 – Frequency Distribution for Passengers

Class (passengers)	Frequency (F) (days)	Midpoint (M)	FM
50 to 59	3	54.5	163.5
60 to 69	7	64.5	451.5
70 to 79	18	74.5	1341.0
80 to 89	12	84.5	1014.0
90 to 99	8	94.5	756.0
100 to 109	2	104.5	208.0
	50		3935.0

Using formula (3.7), it can be seen that P&P flew a daily average of 78.7 passengers.

.

Median

If the data have been recorded in a frequency table, they cannot be placed in an ordered array in order to calculate the median. The Median class of the frequency distribution should be found first. The Median class is that class whose cumulative frequency is greater than or equal to N/2. The Median can be determined as

, (3.8)

Where is the lower boundary of the median class; F is the cumulative frequency of the class preceding the median class; is the frequency of the median class; C is the class interval of the median class.

As an illustration, the frequency table for P&P Airlines is given in Table 3.4

Table 3.4 – Frequency Distribution for Passengers

Class (passengers)	Frequency (F) (days)	Cumulative Frequency (days)
50 to 59	3	3
60 to 69	7	10
70 to 79	18	28
80 to 89	12	40
90 to 99	8	48
100 to 109	2	50

Since N is 50, the median class is the third class in the Table 3.4. It has a cumulative frequency of 28. Using formula (3.8), the median is

.

Conclusion: on 25 days – one-half of the 50 days surveyed – less than 78.33 passengers flew on P&P Airlines, and on the other 25 days more than 78.33 passengers flew the friendly skies of P&P.

Mode

Since by definition the mode is the observation that occurs more often, it will be found in the class with the highest frequency. This class with the largest frequency is called the modal class. To estimate the mode in the case of grouped data, Formula (3.9) is used.

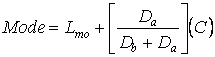, (3.9)

Where is the lower boundary of the median class; is the difference between the frequency of the modal class and the class preceding it; is the difference between the frequency of the modal and the class after it; C is the class interval of the modal class.

< Предыдущая		Следующая >