020. Measures of Central Tendency for Ungrouped Data
There are three common methods of identifying the center of a data set around which the data are located. They are the Mean, the Median, and the Mode. The precise determination of these three values can vary. In each case, that is the point around which all the numbers in the data set seem to be grouped.
Mean
The Mean is the measure of central tendency most commonly thought of as the average. The mean of a population, containing N observations, is calculated as
, (3.1)
Where N is the size of the population.
The mean of population is a parameter. The mean is affected by extreme values, or Outliers.
Example 3.1. Peter wants to compute the mean of his last 10 exams in his statistics course. He adds them up and divide by 10.
If the population as large and it would prove too time-consuming to add up all the observations, the only alternative might be to take a sample and calculate its mean. The mean for a sample is a statistic. It is found as follows:
, (3.2)
Where N is the size of a sample.
Median
The Median is sometimes referred to as the Positional average, because it lies exactly in the middle of the data set after the values have been placed into an ordered array. One-half of the observations will be Above the median, and one-half will be Below the median. Before the median can be calculated, the observations must be put into an ordered array. The median is not affected by extreme value.
In a data set with an Odd number of observations, this middle position is found as
. (3.3)
If there is an Even number of observations, the median is the average of the two middle values.
. (3.4)
Example 3.2. Denny is rightfully worried about his grade in statistics. He scored the following grades on the five tests given this semester: 63, 59, 71, 41, 32. his professor has warned Denny that any grade below 60 is failing. Calculate and interpret Denny’s median grade.
Solution. (1) The values have to be put in an ordered array first. There is no matter if it would be ascending or descending order:
32, 41, 59, 63, 71.
The Position of the median grade is determined as (N+1)/2 = (5+1)/2 = 3. The median is then 59, which is located in the third position after the data have been placed into the ordered array.
(2) Assume a sixth test was given and Denny scored another 63 on it. The ordered array would appear as
32, 41, 59, 63, 63, 71.
The Median position is now (N+1)/2 = (6+1)/2 = 3.5; that is, the third and one-half position. The median is the value halfway between the third and fourth observations, and is therefore (59+63)/2 = 61. This means that half of his test grades were below 61 and half were above 61.
Mode
The Mode is the observation that occurs with the greatest frequency.
From the Example 3.2 (2), the Modal grade is 63 because it occurred more often than any other grade. If still another test was given and Denny managed another 41 on it, the data set would be Bimodal because both 41 and 63 occurred with equal frequency.
If all the observations occur with equal frequency, the data set has no mode.
For the Example 3.2 (1), with Denny’s first five tests of 32, 41, 59, 63, 71, there is no modal grade.
Weighted Mean
In the discussion of the mean in 3.2.1, it was assumed that each observation was equally important. In certain cases, some observations could be given greater weight. The proper procedure is given by Formula 3.4.
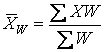, (3.5)
Where 
is the weighted mean; X is the individual observations; W is the weight assigned to each observation.
The weighted mean is higher than the simple arithmetic mean.
Example 3.3. Statistics professor threatens to count the final exam twice as much as the other tests when determining the final grade of each student in the class. Then the score they get on the final must be given twice as much weight. That is, it must be counted twice in figuring the grade. Assume the student scored 89, 92, and 79 on the hour exams, and a 94 on the final exam. These scores and weight can be reflected in Table 3.1. Formula (3.5) yields
.
Table 3.1 – Calculation of the weighted mean
|
Grade (X) |
Weight (W) |
XW |
|
89 |
1 |
89 |
|
92 |
1 |
92 |
|
79 |
1 |
79 |
|
94 |
2 |
188 |
|
Total |
5 |
448 |
This approach is the same as adding the score on the final exam twice in computing the average:
.
Example 3.4. Paul the Plumber sells five types of drain cleaner. Each type, along with the profit per can and the number of cans sold, is shown in Table 3.2.
Table 3.2 – Types of Drain Cleaner for Paul the Plumber
|
Cleaner |
Profit per Can (X), $ |
Sales Volume in Cans (W) |
XW, $ |
|
Glunk Out |
2.00 |
3 |
6.00 |
|
Bubble Up |
3.50 |
7 |
24.50 |
|
Dream Drain |
5.00 |
15 |
75.00 |
|
Clear More |
7.50 |
12 |
90.00 |
|
Main Drain |
6.00 |
15 |
90.00 |
|
24.00 |
52 |
285.50 |
Solution. The simple arithmetic mean of Paul’s profit can be calculated as $24/5 = $4.80 per can. This is not a good estimate of Paul’s average profit, since he sells more of some types than he does of others. In order to get a financial statement more representative of his true business performance, Paul must give more weight to the more popular types of cleaner. The proper calculation would therefore be the weighted mean. The proper measure of weight would be the amounts sold. The weighted mean is then
per can.
Interpretation. In this example the weighted mean is higher than the simple arithmetic mean because Paul sells more of those types of cleaner with a higher profit margin.
| < Предыдущая | Следующая > |
|---|
