5.2.1. Факторный анализ

Итак, из условия представленной выше задачи следует, что у нас есть массив дан­ных, состоящий из 24 независимых переменных (утверждений), в различных ас­пектах описывающих текущее состояние авиакомпании X на международном рынке авиаперевозок. Основной задачей проводимого факторного анализа является груп­пировка схожих по смыслу утверждений в макрокатегории с целью сократить чис­ло переменных и оптимизировать структуру данных.

При помощи меню Analyze ►Data Reduction ► Factor вызовите окно Factor Analysis. Пе­ренесите из левого списка в правый переменные для анализа (ql-q24), как показа­но на рис. 5.32. Поле Selection Variable позволяет выбрать переменную, в разрезе которой будет проводиться анализ (например, класс полета). В нашем случае ос­тавьте это поле Пустым.

Щелкните на кнопке Descriptives и в открывшемся диалоговом окне (рис. 5.33) вы­берите пункт КМО and Barlett's test of sphericity. Это позволит определить, насколько имеющиеся данные пригодны для факторного анализа. Окно Descriptives позволя­ет вывести и другие необходимые описательные статистики. Однако в большин­стве примеров из маркетинговых исследований эти возможности, как правило, не используются.

 

Закройте окно Descriptives, щелкнув на кнопке Continue. Далее откройте окно Extraction (рис. 5.34), щелкнув на соответствующей кнопке в главном диалоговом окне Factor Analysis. Это окно предназначено для выбора метода формирования факторной модели; выполните в нем следующие действия.

Рис. 5.34. Диалоговое окно Extraction

 

Во-первых, в поле Method выберите метод извлечения (формирования) факторов. Общая рекомендация по выбору метода состоит в следующем. Необходимо выби­рать тот метод извлечения факторов, который позволяет однозначно классифицировать как можно больше переменных. Таким образом, основные соображения здесь — число классифицированных факторов и однозначность классификации (то есть каждая переменная должна принадлежать только одному фактору). Как вы увидите ниже, установленный по умолчанию в SPSS метод Principal components в нашем случае позволяет однозначно классифицировать 22 переменные из 24 име­ющихся (92 %), что является весьма хорошим показателем. На основании имею­щегося опыта автор может утверждать, что хорошим результатом факторного ана­лиза является доля однозначно классифицированных переменных не менее 90 %. Выберите метод Principal components. Данный метод является наиболее подходя­щим для решения большинства задач маркетинговых исследований при помощи факторного анализа.

Во-вторых, укажите количество образуемых факторов (группа Extract). По умол­чанию установлен метод определения количества извлекаемых факторов на осно­вании значений характеристических чисел (Eigenvalues over). He вдаваясь в стати­стические тонкости, отметим, что характеристические числа используются SPSS для определения количественного и качественного состава извлекаемых факто­ров. При предустановленном значении данного показателя, равном 1, количество образуемых факторов будет равно количеству переменных, значение характерис­тических чисел для которых больше или равно 1.

Также существует возможность вручную указать программе, сколько факторов необходимо извлекать (Number of factors). Эта возможность предусмотрена в SPSS для того, чтобы при слишком большом количестве переменных с характеристи­ческим числом больше 1 вручную сократить число факторов. Большое число фак­торов трудно интерпретировать, поэтому если методом характеристических чисел не удается извлечь приемлемое для интерпретации число факторов (чем меньше, тем лучше), следует самостоятельно указать программе число факторов. Эта зада­ча решается аналитиком в каждом конкретном случае индивидуально. В качестве одного из вариантов решения можно рекомендовать увеличить число eigenvalue с предустановленного значения 1, скажем, до 1,5 или более. Это поможет, если по­лучено большое число факторов с характеристическим числом, приблизительно равным 1, и несколько (2-3 и более) факторов — с характеристическим числом более 1,5 или другого значения. Также при ручном определении количества фак­торов аналитик может принять релевантное решение, основываясь на своем опыте или на каких-либо иных предположениях. И наконец, необходимо отметить, что при ручном указании числа извлекаемых факторов иногда количество однознач­но классифицированных переменных оказывается меньше, чем при методе экст­ракции по величине характеристических чисел. Однако данный негативный мо­мент нивелируется возросшей наглядностью результатов факторного анализа — ведь это позволяет освободиться от факторов, в которых нет переменных со значи­мым коэффициентом корреляции (в нашем случае 0,5).

Закройте диалоговое окно Extraction, щелкнув на кнопке Continue. Выберите тип ротации матрицы коэффициентов (кнопка Rotation в главном диалоговом окне Factor Analysis). Ротация коэффициентной матрицы производится для того, чтобы мак­симально приблизить факторную модель к идеалу: возможности однозначно клас­сифицировать все переменные. В диалоговом окне Rotation (рис. 5.35) выберите конкретный метод ротации. В большинстве случаев наиболее приемлемым вари­антом является метод Varimax. Он облегчает интерпретацию факторов, минимизируя количество переменных с высокими факторными нагрузками. Выберите этот тип ротации и закройте диалоговое окно, щелкнув на кнопке Continue.

Рис. 5.35. Диалоговое окно Rotation

Далее откройте диалоговое окно Factor Scores (рис. 5.36), щелкнув на кнопке Scores. Это окно служит для создания в исходном файле данных новых переменных, ко­торые в дальнейшем позволят отнести каждого респондента к определенной груп­пе (фактору). Число вновь создаваемых переменных равно числу извлеченных факторов. Ниже мы покажем, каким образом использовать данные переменные. Выберите в диалоговом окне Factor Scores параметр Save as variables, а в качестве метода определения значений для этих новых переменных — регрессионную мо­дель Regression. После этого закройте диалоговое окно, щелкнув на кнопке Continue.

Рис. 5.36. Диалоговое окно Factor Scores

Последним этапом перед запуском процедуры факторного анализа является вы­бор некоторых дополнительных параметров (кнопка Options). В открывшемся ди­алоговом окне (рис. 5.37) выберите два пункта: Sorted by size и Suppress absolute values less than. Первая опция позволяет вывести переменные, входящие в каждый фак­тор, в порядке убывания их факторных коэффициентов (величины вклада пере­менной в формирование фактора). Вторая оказывается весьма полезна, так как облегчает задачу однозначной интерпретации полученных факторов. Указанное в соответствующем поле значение данного параметра (в нашем случае 0,5) отсекает переменные с факторными коэффициентами менее данного значения. Это позво­ляет упростить ротированную матрицу факторов, поскольку из нее исчезают не­значимые переменные, входящие в каждый извлеченный фактор. Если вы не за­действуете данный параметр, для каждой переменной будет отображен факторный коэффициент по каждому фактору, что излишне перегрузит факторную модель и затруднит ее восприятие исследователями.

Параметр Suppress absolute values less than вводится, чтобы облегчить практическую интерпретацию результатов факторного анализа. Так как факторные коэффици­енты в результирующей ротированной матрице коэффициентов являются коэф­фициентами корреляции между соответствующими переменными и факто­рами, в большинстве практических случаев целесообразно устанавливать начальное значение отсечения незначимых переменных на уровне 0,5. Если в результате фак­торного анализа окажется, что число классифицированных переменных менее при­емлемого (например, если структура данных не вполне подходит для факторного анализа; см. ниже), можно пересчитать факторную модель с меньшим значением отсечения (например, 0,4). В обратной ситуации, если переменная входит в не­сколько факторов, можно предложить повысить уровень экстракции с 0,5 до 0,6. Это позволит устранить переменные, входящие сразу в несколько факторов, уве­личив практическую пригодность результатов факторного анализа.

Итак, указав все необходимые параметры в окне Options, закройте его (кнопка Continue) и запустите процедуру факторного анализа при помощи щелчка на кноп­ке 0К в главном диалоговом окне Factor Analysis.

Рис. 5.37. Диалоговое окно Options

После того как программа произведет все необходимые расчеты, откроется окно SPSS Viewer с результатами построения факторной модели. Первое, что нас инте­ресует, — это пригодность имеющихся данных для факторного анализа в целом. Посмотрим на таблицу КМО and Barlett's Test (рис. 5.38). В ней есть два интересую­щих нас показателя: тест КМО и значимость теста Barlett. Результаты теста КМО позволяют сделать вывод относительно общей пригодности имеющихся данных для факторного анализа, то есть насколько хорошо построенная факторная модель описывает структуру ответов респондентов на анализируемые вопросы. Результа­ты данного теста варьируются в интервале от 0 (факторная модель абсолютно не­применима) до 1 (факторная модель идеально описывает структуру данных). Фак­торный анализ следует считать пригодным, если КМО находится в пределах от 0,5 до 1. В нашем случае этот показатель равен 0,9, что является весьма хорошим ре­зультатом.

Barlett's test of sphericity проверяет гипотезу о том, что переменные, участвующие в факторном анализе, некоррелированы между собой. Если данный тест дает по­ложительный результат (переменные некоррелированы), факторный анализ сле­дует признать непригодным использовать другие статистические методы (на­пример, кластерный анализ). Статистикой, определяющей пригодность факторного анализа по тесту Barlett, является значимость (строка Sig.). При приемлемом уровне

Значимости (ниже 0,05) факторный анализ считается пригодным для анализа ис­следуемой выборочной совокупности. В нашем случае рассматриваемый тест по­казывает весьма низкую значимость (менее 0,001), из чего следует вывод о приме­нимости факторного анализа.

Итак, на основании тестов КМО и Barlett мы пришли к выводу, что имеющиеся у нас данные практически идеально подходят для исследования при помощи фак­торного анализа.

Рис. 5.38. Таблица КМО and Barlett s Test

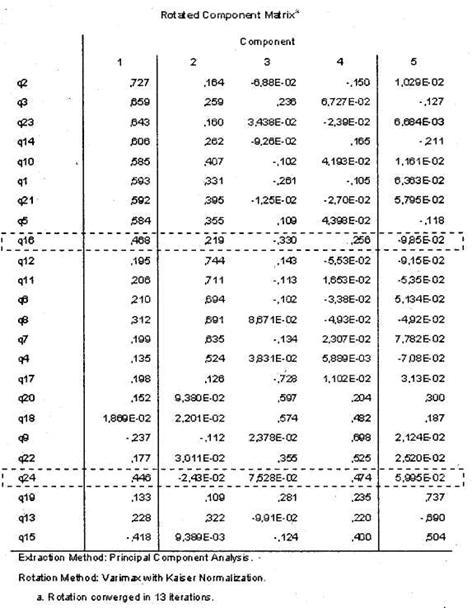
Следующим шагом в интерпретации результатов факторного анализа является рассмотрение результирующей ротированной матрицы факторных коэффициен­тов: таблицы Rotated Component Matrix (рис. 5.39). Данная таблица является основ­ным результатом факторного анализа. В ней отражаются результаты классифика­ции переменных по факторам. В нашем случае при помощи автоматического метода определения количества факторов (на основании характеристических чисел боль­ше 1) была построена практически приемлемая факторная модель, в которой 22 из 24 переменных удалось однозначно классифицировать по небольшому числу фак­торов (5). Данный результат может считаться хорошим.

С неклассифицированными переменными можно поступить следующим образом. Необходимо просто пересчитать факторную модель, удалив в диалоговом окне Options ранее установленное значение отсечения 0,5. Далее будет построена фак­торная матрица (рис. 5.40), в которой аналитику предстоит самостоятельно опре­делить принадлежность неклассифицированных переменных к тому или иному фактору на основании критерия наибольшего коэффициента корреляции между переменными и пятью факторами. В нашем случае вы видите, что переменная ql6 в наибольшей степени коррелирует с фактором 1 (факторный коэффициент 0,468) и, следовательно, должна быть отнесена к данному фактору, а переменная q24 — с фактором 4 (0,474).

После того как мы однозначно классифицировали все переменные, вернемся к таб­лице на рис. 5.40. Мы получили пять групп переменных (факторов), описываю­щих текущую конкурентную позицию авиакомпании X с пяти различных сторон. Вот эти группы.

Фактор 1

Q2. Авиакомпания X может конкурировать с лучшими авиакомпаниями мира. q3. Я верю, что у авиакомпании X есть перспективное будущее в мировой авиации. q23. Авиакомпания X — лучше, чем многие о ней думают. q!4. Авиакомпания X — лицо России.

Рис. 5.39. Таблица Rotated Component Matrix

QlO. Авиакомпания Х действительно заботится о пассажирах.

Ql. Авиакомпания X обладает репутацией компаний, превосходно обслуживающей пасса­жиров.

Q21. Авиакомпания X — эффективная авиакомпания. q5. Я горжусь тем, что работаю в авиакомпании X.

Ql6. Обслуживание авиакомпании X является последовательным и узнаваемым во всем мире.

Фактор 2

Ql2. Я верю, что менеджеры высшего звена прикладывают все усилия для достижения успеха авиакомпании.

Qll. Среди сотрудников авиакомпании имеет место высокая степень удовлетворенности работой.

Q6. Внутри авиакомпании X хорошее взаимодействие между подразделениями.

Рис. 5.40. Таблица Rotated Component Matrix, содержащая все факторные коэффициенты

 

Q8. Сейчас авиакомпания X быстро улучшается.

Q7. Каждый сотрудник авиакомпании прикладывает все усилия для того, чтобы обеспе­чить ее успех.

Q4. Я знаю, какой будет стратегия развития авиакомпании X в будущем.

Фактор 3

Ql7. Я бы не хотел, чтобы авиакомпания X менялась.

Q20. Изменения в авиакомпании X будут позитивным моментом.

Ql8. Авиакомпании X необходимо меняться для того, чтобы использовать в полной мере имеющийся потенциал.

Фактор 4

Q9. Нам предстоит долгий путь, прежде чем мы сможем претендовать на то, чтобы назы­ваться авиакомпанией мирового класса.

Q22. Я бы хотел, чтобы имидж авиакомпании X улучшился с точки зрения иностранных пассажиров.

Q24. Важно, чтобы люди во всем мире знали, что мы — российская авиакомпания.

Фактор 5

Ql9. Я думаю, что авиакомпании X необходимо представить себя в визуальном плане бо­лее современно.

Ql3. Мне нравится, как в настоящее время авиакомпания X представлена визуально широ­кой общественности (в плане цветовой гаммы и фирменного стиля).

Ql5. Мы выглядим «вчерашним днем» по сравнению с другими авиакомпаниями.

Наиболее сложной задачей при проведении факторного анализа является интер­претация полученных факторов. Здесь не существует какого-либо универсально­го решения: в каждом конкретном случае, аналитик использует имеющийся прак­тический опыт для того, чтобы понять, почему факторная модель относит ту или иную переменную к данному конкретному фактору. Бывают случаи (особенно при малом числе хорошо формализованных переменных), когда образованные факто­ры являются очевидными и различия между переменными видны невооруженным глазом. В такой ситуации можно обойтись без факторного анализа и разбить пере­менные на группы вручную. Однако эффективность и мощь факторного анализа проявляются в сложных и нетривиальных случаях, когда переменные нельзя зара­нее классифицировать, а их формулировки запутаны. Тогда большой исследова­тельский интерес будет вызывать классификация переменных именно на основа­нии мнений респондентов, что позволит выявить то, как сами опрошенные поняли тот или иной вопрос.

Приводим рекомендации, которые помогут вам при затруднении интерпретиро­вать результаты факторного анализа.

Когда это возможно и приемлемо для целей исследования, следует формализо­вать переменные до проведения факторного анализа. Это позволит аналитику за­ранее сделать предположения о разделении совокупности имеющихся перемен­ных на группы. Задача исследователя при интерпретации результатов факторной матрицы в данном случае упростится, так как он уже не будет начинать «с чистого листа». Его задача сведется к проверке ранее выдвинутых гипотез о принадлежно­сти той или иной переменной к конкретной группе.

Иногда возникают случаи, когда переменная, отнесенная SPSS к конкретному фактору, логически никак не связана с остальными переменными, составляющи­ми тот же фактор. Можно пересчитать факторную модель без отсечения незначи­мых коэффициентов (как в примере на рис. 5.40) и посмотреть, с каким еще факто­ром данная нелогичная переменная коррелирует практически с той же силой, как с фактором, к которому она была отнесена автоматически. Например, переменная Z имеет коэффициент корреляции с фактором 1, равный 0,505, а с фактором 2 она коррелирует с коэффициентом 0,491. SPSS автоматически относит данную пере­менную к тому фактору, с которым выявлена наибольшая корреляция, не учиты­вая при этом, что с другим фактором данная переменная коррелирует практически с той же силой. Именно в такой ситуации (при небольшой разнице в коэффициен­тах корреляции) можно попробовать отнести переменную Z к фактору 2, и если это окажется логичным, рассматривать ее в группе переменных из второго фактора.

Можно вручную сократить число извлекаемых факторов, что облегчит задачу ис­следователя при интерпретации результатов факторного анализа. Однако необхо­димо иметь в виду, что такое сокращение снизит гибкость факторной модели и даже может привести к ситуации, когда переменные будут ложно разделены на неверные, с практической точки зрения, группы. Также снижение числа извлекае­мых факторов неизбежно снизит и долю однозначно классифицированных факто­ров.

В качестве варианта предыдущего решения можно предложить объединить два или более факторов с небольшими количествами входящих в них переменных. Такая группировка, с одной стороны, позволит снизить число интерпретируемых факто­ров, а с другой — облегчит понимание малочисленных факторов.

Если исследователь зашел в тупик и никакие средства не помогают объяснить при­надлежность той или иной переменной к конкретному фактору, остается приме­нить другую статистическую процедуру (например, кластерный анализ).

Вернемся к нашим пяти факторам. Задача их описания и объяснения представля­ется не очень сложной. Так, можно заметить, что утверждения, входящие в первый фактор (q2, q3, q23, ql4, qlO, ql, q21, q5 и ql6), являются общими, то есть касаются всей авиакомпании и описывают отношение к ней со стороны авиапассажиров. Единственное исключение составила переменная q5, имеющая отношение скорее ко второму фактору. Коэффициент корреляции с фактором 2 — 0,355 (см. рис. 5.40), что позволяет отнести его в данную группу из соображений логики. Фактор 2 (ql2, qll, q6, q8, q7 и q4) описывает отношение к авиакомпании X со стороны сотрудни­ков. Третий фактор (ql7, q20 и ql8) описывает отношение респондентов к измене­ниям в авиакомпании (в него попали все утверждения, имеющие корень «мен» — от слова «изменение»). Четвертый фактор (q9, q22 и q24) описывает отношение респондентов к имиджу авиакомпании. Наконец, пятый фактор (ql9, ql3 и ql5) объединяет утверждения, характеризующие отношение респондентов к визуаль­ному образу авиакомпании X.

Таким образом, мы получили пять групп утверждений, описывающих текущую конкурентную позицию компании X на международном рынке авиаперевозок. На основании проведенного интерпретационного (семантического) анализа можно присвоить данным группам (факторам) следующие определения.

■ Фактор 1 характеризует общее положение авиакомпании X в глазах ее клиентов.

■ Фактор 2 характеризует внутреннее состояние авиакомпании X с точки зрения ее сотрудников.

■ Фактор 3 характеризует изменения, происходящие в авиакомпании X.

■ Фактор 4 характеризует имидж авиакомпании X.

■ Фактор 5 характеризует визуальный образ авиакомпании X.

После того как мы успешно интерпретировали все полученные факторы, можно считать факторный анализ завершенным и удавшимся. Далее мы покажем, как можно использовать результаты факторного анализа для построения разрезов.

Вспомним о том, что мы сохранили факторные рейтинги (то есть принадлежность каждого респондента к определенному фактору) в исходном файле данных в виде новых переменных. Эти переменные имеют имена типа: facX_Y, где X — это номер фактора, a Y — порядковый номер факторной модели. Если мы строили факторную модель дважды и в результате в первый раз было извлечено три фактора, а во второй — два, имена переменных будут следующими:

■ facl_l, fac2_l, fac3_l (для трех факторов из первой построенной модели);

■ facl_2, fac2_2 (для двух факторов из второй модели).

В нашем случае будет создано пять новых переменных (по числу извлеченных фак­торов). Эти факторные рейтинги в дальнейшем могут использоваться, например, для построения разрезов. Так, если необходимо выяснить, каким образом респон­денты — мужчины и женщины — оценивают различные стороны деятельности авиа­компании X, это можно сделать при помощи анализа факторных рейтингов.

Наиболее частый способ использования факторных рейтингов в дальнейших рас­четах — это ранжирование и последующее разделение вновь созданных перемен­ных, обозначающих извлеченные факторы, на четыре квартиля (25%-проценти-ля). Такой подход позволяет создать новые переменные с порядковой шкалой, описывающие четыре уровня каждого фактора. В нашем случае для утверждений, составляющих фактор 2, такими уровнями будут: не согласен (состояние внутрен­них дел компании не удовлетворяет сотрудников), скорее не согласен (оценка внут­ренней ситуации в компании ниже среднего), скорее согласен (оценка выше сред­него), согласен (оценка отлично).

Чтобы создать переменные, по которым далее будут группироваться респонденты, вызовите меню Transform ► Rank Cases. В открывшемся диалоговом окне (рис. 5.41) из левого списка выберите переменную, содержащую факторные рейтинги для фактора 2 (fac2_l), и поместите ее в поле Variables. Далее в области Assign Rank I to выберите пункт Smallest value, в нашем случае это означает, что первую группу (не согласен) составят респонденты, оценивающие состояние внутренних дел авиаком­пании как плохое. Соответственно группы 2, 3 и 4 будут определены для катего­рий скорее не согласен, скорее

согласен и согласен соответственно.

Рис. 5.41. Диалоговое окно Rank Cases

Щелкните на Rank Types ► Types, отмените установленный по умолчанию параметр Rank и вместо него выберите Ntiles с предустановленным числом групп, равным 4 (рис. 5.42). Щелкните на кнопке Continue и затем в главном диалоговом окне на ОК. Данная процедура создаст в файле данных новую переменную nfac2_l (2 означает второй фактор), распределяющую респондентов на четыре группы.

Рис. 5.42. Диалоговое окно Types

Все респонденты в выборке характеризуются положительным, скорее положитель­ным, скорее отрицательным или отрицательным отношением к текущему состоя­нию дел в авиакомпании X. Для повышения наглядности рекомендуется присво­ить метки каждому из выделенных четырех уровней; можно переименовать и саму переменную. Теперь вы можете проводить перекрестный анализ при помощи но­вой порядковой переменной, а также строить другие статистические модели, пре­дусмотренные в SPSS. Ниже будет показано, как использовать результаты постро­ения факторной модели в кластерном анализе.

Для иллюстрации возможностей практического использования новой переменной проведем перекрестный анализ влияния пола респондентов на их оценку текуще­го состояния дел в авиакомпании X (рис. 5.43). Как следует из представленной таблицы, респонденты-мужчины в целом склонны ставить более низкие оценки рассматриваемому параметру авиакомпании по сравнению с женщинами. Так, в структуре оценок очень плохо, плохо и удовлетворительно доля мужчин преобладает; в оценках очень хорошо, напротив, преобладают женщины. При переходе в каждую следующую (более высокую) категорию оценок доля мужчин равномерно убыва­ет, а доля женщин, соответственно, возрастает. Тест %2 показывает, что выявлен­ная зависимость является статистически значимой.

Рис. 5.43. Перекрестное распределение: влияние пола респондентов на их оценку текущего состояния дел в авиакомпании X

< Предыдущая		Следующая >