4.2.1. Исследование линейных корреляций по Пирсону, Спирману и Кендалу

Сначала мы рассмотрим пример применения коэффициента корреляции Пирсо­на. Предположим, что у нас есть ответы респондентов на следующие два вопроса. Каков Ваш среднемесячный доход в расчете на одного члена семьи? с вариантами ответа:

■ до $100;

■ от $ 100 до $ 300;

■ от $ 300 до $ 600;

■ от $ 600 до $ 1000;

■ от $ 1000 до $ 1500;

■ свыше $1500.

Как часто Вы посещаете рестораны? с вариантами ответа:

■ более 1 раза в день;

■ примерно 1 раз в день;

■ 2-3 раза в неделю;

■ примерно 1 раз в неделю;

■ 2-3 раза в месяц;

■ примерно 1 раз в месяц;

■ реже 1 раза в месяц.

В результате ввода в компьютер заполненных анкет респондентов были получены две переменные: q3 (первый вопрос) и q28 (второй вопрос). Необходимо устано­вить, зависит ли частота посещения ресторанов от дохода респондентов, и если да, то каким образом. В связи с тем, что в ходе опроса при ответе на каждый вопрос респондентам предлагалось на выбор несколько вариантов ответа, тип шкалы у полученных переменных получился порядковым (в файле данных есть только коды ответов, но не сами числовые значения, отражающие частоту посещения рестора­на или уровень дохода).

Далее мы рассмотрим не только как использовать коэффициент корреляции Пир­сона, но также как использовать данный коэффициент для анализа квазипорядко­вых переменных. Дело в том, что некоторые переменные, хотя они и закодированы как порядковые, по сути являются интервальными (как в нашем случае). Это де­лается специально, чтобы, с одной стороны, увеличить долю респондентов, от­ветивших на вопрос, а с другой стороны, уменьшить число возможных ошибок при вводе в компьютер текстовых полей (для открытых вопросов). Интервалы также полезны при анализе, поскольку нет необходимости кодировать текстовые (или интервальные) переменные, а можно сразу увидеть группы (интервалы) значений. Практика показывает, что подобное составление анкет для маркетинговых иссле­дований является стандартным, поэтому корреляционный анализ редко проводится на изначально интервальных переменных (текстовые поля анкеты).

Для описываемых квазипорядковых переменных следует применять именно ко­эффициент корреляции Пирсона. Использование коэффициентов Спирмана или Кендала в этом случае является некорректным. Более подробно эти два коэффи­циента представлены ниже; пока же в общих чертах о них можно сказать следую­щее. Коэффициенты Спирмана или Кендала показывают только степень соответ­ствия порядка следования вариантов ответа в ранжированных списках (есть отсутствие инверсий). При этом корреляции по Спирману и Кендалу используют­ся в основном, когда элементы ранжированных списков представлены мнемони­ческими, а не числовыми константами. Таким образом, данные коэффициенты не помогут нам в характеристике зависимости между частотой посещения рестора­нов и доходом респондентов. Однако в нашем случае нельзя применять и коэффи­циент корреляции Пирсона, так как в этом случае анализировались бы коды ин­тервалов (1 -6 — в первом вопросе и 1 -7 — во втором), а не действительные ответы респондентов на вопросы1.

Итак, сначала мы должны преобразовать имеющиеся у нас порядковые перемен­ные к интервальному виду. Лучше всего сделать это при помощи замены кодов интервалов (1-6) на средние значения данных интервалов. Например, среднее зна­чение для интервала 3 в переменной q3 — это $ 450 (450 = (300 + 600) / 2). Преоб­разовав обе переменные к данному виду, мы получим следующие интервальные переменные q3_i и q28_i (табл. 4.5)2.

Таблица 4.5. Схема перекодировки порядковых переменных (q3 и q28) в интервальные (q3_i и q28_i)

Порядковые переменные	Интервальные переменные
Каков Ваш среднемесячный доход в расчете на одного члена семьи?
До $ 100	$50
От $ 100 до $ 300	$200
От $ 300 до $ 600	$450
От $ 600 до $ 1000	$ 800
От $ 1000 до $ 1500	$ 1250
Свыше $ 1500	$ 1750
Как часто Вы посещаете рестораны?
Более 1 раза в день	60 раз в месяц
Примерно 1 раз в день	30 раз в месяц
2-3 раза в неделю	10 раз в месяц
Примерно 1 раз в неделю	4 раза в месяц
2-3 раза в месяц	2,5 раза в месяц
Примерно 1 раз в месяц	1 раз в месяц
Реже 1 раза в месяц	0,5 раза в месяц

Теперь мы можем приступить непосредственно к корреляционному анализу (опи­санию зависимости между частотой посещения ресторанов и уровнем дохода). Для этого выберите пункт меню Analyze ► Correlate ► Bivariate. В открывшемся диалого­вом окне (рис. 4.17) выберите в левом списке всех доступных переменных две ин­тересующие нас (q3_i и q28_i) и перенесите их в область Variables. Остальные пара­метры в этом диалоговом окне, установленные по умолчанию, следует оставить неизменными: вывод коэффициентов корреляции Пирсона (параметр Pearson в области Correlation Coefficients) и статистической значимости коэффициентов (па­раметр Two-tailed в области Test of Significance). Кнопка Options не предлагает иссле­дователю каких-либо существенных параметров. Чтобы запустить процедуру по­строения корреляционной таблицы, щелкните на кнопке ОК.

Рис. 4.17. Диалоговое окно Bivariate Correlations (корреляция Пирсона)

 

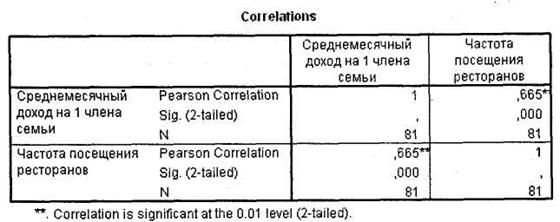
В окне SPSS Viewer появится таблица Correlations с результатами расчетов коэффи­циента корреляции Пирсона и статистической значимости данного коэффициента. Как видно из рис. 4.18, в нашем случае коэффициент корреляции Пирсона между двумя исследуемыми переменными (q3_i и q28_i) равен +0,665, а его статистическая значимость меньше 0,001. Следовательно, можно сделать вывод о том, что между среднемесячным доходом респондентов и частотой посещения ими ресторанов су­ществует статистически значимая умеренная (средняя) линейная возрастающая за­висимость. То есть частота посещения ресторанов в достаточно высокой степени (коэффициент Пирсона = 0,7) зависит от уровня доходов потребителей, причем при росте среднемесячного дохода частота посещения ресторанов линейно возрастает.

Существует возможность проводить корреляционный анализ сразу для нескольких переменных. Для этого необходимо поместить эти переменные в область Variables диалогового окна Bivariate Correlations. В таблице Correlations будут показаны коэф­фициенты корреляции для каждой пары исследуемых переменных.

Теперь рассмотрим процедуру проведения корреляционного анализа при помощи ранговых коэффициентов Спирмана и Кендала. В данных методах одна перемен­ная (эталонная) представлена в виде ранжированной последовательности мнемо­нических категорий, а другой переменной присваиваются ранговые места. Корре­ляционные коэффициенты рассчитываются исходя из количества инверсий, то есть числа нарушений порядка следования рангов по сравнению с первым рядом. В большинстве случаев рекомендуется применять коэффициент корреляции Спирмана. Использование коэффициента Кендала оправдано только в том случае, когда в структуре данных имеются выбросы.

Рис. 4.18. Таблица Correlations (корреляция Пирсона)

 

В практике маркетинговых исследований наиболее часто коэффициенты корре­ляции Спирмана применяются для анализа не всей выборочной совокупности рес­пондентов (базы данных в целом), а агрегированных ранжированных перечней, полученных в результате других преобразований1. Приведем пример. Предположим, что в результате опроса посетителей магазинов одежды были по­лучены ответы на следующие два вопроса. Какие факторы для Вас наиболее важны при выборе одежды? с вариантами ответа:

■ Высокое качество одежды.

■ Доступные цены.

■ Широта ассортимента одежды.

■ Близость к дому или работе.

■ Высокое качество обслуживания.

■ Красивый интерьер магазина.

Оцените, пожалуйста, следующие характеристики данного магазина одежды (в котором происходит опрос) по пятибалльной шкале (от 1 — очень плохо до 5 — отлично) с ва­риантами ответа:

■ Высокое качество одежды.

■ Доступные цены.

■ Широта ассортимента одежды.

■ Близость к дому или работе.

■ Высокое качество обслуживания.

■ Красивый интерьер магазина.

■ Ваша общая оценка работы данного магазина.

Над результатами второго вопроса был проведен множественный линейный рег­рессионный анализ. Анализировалось влияние оценок частных параметров всех исследованных магазинов одежды на их общую оценку. В разделе 4.3 подробно рассматривается процедура линейного регрессионного анализа, позволяющая, в частности, построить ранжированный перечень частных параметров по силе их влияния на общую оценку.

Таким образом, были получены два ранжированных списка с одинаковыми катего­риями: две схемы выбора магазина одежды. Затем оба списка были введены в SPSS под кодами, представленными выше: от 1 (наиболее важный фактор) до 6 (наименее важный фактор) (рис. 4.19). На рис. 4.20 представлены данные списки в мнемони­ческой форме. Первый список представлен в переменной sc_l; второй — в sc_2.

Рис. 4.19. Окно SPSS Data Editor с двумя ранжированными перечнями наиболее значимых для респондентов факторов выбора магазинов одежды

Рис. 4.20. Окно SPSS Data Editor с двумя ранжированными перечнями наиболее значимых для респондентов факторов выбора магазинов одежды одежды

 

Как вы видите на рис. 4.20, две схемы выбора, составленные на основании прямого метода (вопрос 1) и на основании регрессионного анализа (вопрос 2), соответству­ют друг другу не полностью, различаясь в порядке следования первой и второй категорий. Проанализируем эти схемы выбора магазинов одежды на предмет со­ответствия при помощи коэффициента корреляции Спирмана.

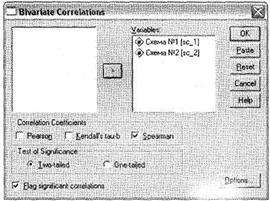Для этого снова откройте диалоговое окно Bi variate Correlations, выбрав пункт меню Analyze ► Correlate ► Bivariate. Перенесите две интересующие нас переменные — Схе­ма №1 (составленная по вопросу 1) и Схема №2 (составленная по вопросу 2) — из левого списка всех доступных переменных в область Variables (рис. 4.21). Отмени­те вывод корреляции Пирсона и вместо него выберите параметр Spearman (корре­ляция Спирмана). После этого начните расчет при помощи щелчка на кнопке ОК.

Рис. 4.21. Диалоговое окно Bivariate Correlations (корреляция Спирмана)одежды

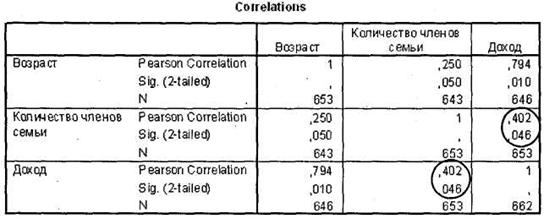В окне SPSS Viewer появится таблица Correlations с результатами расчета коэффи­циента ранговой корреляции (Спирмана) по двум анализируемым переменным. Как следует из рис. 4.22, две рассматриваемые схемы выбора различаются несуще­ственно. Данный вывод можно сделать из сильной корреляции между переменны­ми sc_l и sc_2 (коэффициент корреляции Спирмана = 0,9), характеризующейся весьма высокой статистической значимостью (0,005).

Рис. 4.22. Таблица Correlations (корреляция Спирмана)

В заключение напомним, что ранговый коэффициент корреляции Спирмана (в от­личие от Кендала) может применяться и в качестве аналога корреляции Пирсона при исследовании зависимостей между переменными, не приводимыми к интер­вальному виду и потому не являющимися ранжированными списками. В качестве примера можно привести гипотетический случай, рассмотренный выше, когда анализируется влияние пола респондентов (дихотомическая шкала) на уровень обра­зования (порядковая по сути, но номинальная по виду шкала).

< Предыдущая		Следующая >