Предметный указатель
А
Абсцисса 16 Алгебра событий 520
- борелевская (о-алгебра) 520 Алгебраическая линия и-го порядка 19
- форма комплексного числа 128 Алгебраический многочлен 137 Алгебраическое дополнение 106
- уравнение и-ой степени 142 Альтернирование тензоров 487 Аппликата 15
Аргумент комплексного числа 132
- функции у = f(x) 200
- промежуточный 223,313 Аргументы функции z = f(x, у) 303 —у =f(xi, x2,...,xj 303 Аснмпшга(ы) 245
- вертикальная 245
- гиперболы 27
- графика функции 246
- наклонная 246 Астроида 46
Аффинные координаты 70
Базис 69
- евклидова пространства 158
- линейного пространства 153
- ортогональный 160
- ортонормированный 160 Бесконечно малые функции 207
- высшего порядка 208
- k-го порядка 208
- несравнимые 209
- одного порядка 208
- равносильные (эквивалентные) 208 Бета-функция (эйлеров интеграл первого
Рода) 291 Бином Ньютона 234
Валентность тензора (ранг) 485 Варианта 538
Вариантный ряд дискретный 538 Вектор 4, 55,150
- единичный 55,59
- касательной к линии 257
— нормали к поверхности 317
— нормированный 160
— нулевой 55
— переменный 253
Векторная линия (силовая линия) 475 - трубка 475 Векторное поле 475
— одномерное 475
— осеснмметрическое 475
— плоскопараллельное 475
— потенциальное 480
— соленоид альное (трубчатое) 476
— цилиндрическое 475
Векторное произведение двух векторов 65 Вектор-функция 253
— дифференцируемая 255
— непрерывная 254 Векторы базисные 60,153
— коллинеарные 55
— линейного пространства 152
— компланарные 56
— линейного пространства 153
— линейного пространства 150 - ортогональные 160
— противоположные 56 - равные 55
— составляющие (компоненты) 59 Величина направленного отрезка 4
/ Вероятность события 519
— аксиоматическая 520
— геометрическая 519
— классическая 519
— статистическая 520
— условная 522 Версьера (локон Аньезн) 41 Взаимное расположение двух плоскостей 81 ---прямых 83
— прямой н плоскости 86 Винтовая линия 74
Выборка (выборочная совокупность) 538 Выборочная дисперсия 540
— средняя 539 Выборочный метод 538 Выпуклость графика функции 244 Вычет функции 573 Вычисление объемов тел 298
— площадей плоских областей 292,330 .
— поверхностей 299,337
Гамма-функция (эйлеров интеграл второго рода) 290 Геликоид 97
Генеральная дисперсия 539
- совокупность 538
- средняя 539
Генеральное среднее квадратическое отклонение 539 Геометрический смысл дифференциала 230
- интеграла двойного 321 ---определенного 279
- модуля и аргумента производной/^) 554
- полного дифференциала функции двух переменных 308
- производной 220
- частной производной 306 Гипербола 27
- параметрические уравнения 31,32
- уравнение, отнесенное к вершине 31
- уравнение относительно асимптот 31
- равносторонняя 27
Ги пербо лический косинус 218
- котангенс 218 - синус 218 - тангенс 218
Г иперболоид вращения двуполостный 90 —однополостный 90
- дауполостный 91
- однополостный 91 Гипотрохоида 47 Гипоциклоида 47
Годограф вектор-функции 253 Гомоморфизм групп 198 Градиент скалярного поля 472 Грань последовательности верхняя 203
- нижняя 204
- числового множества верхняя 302
- - нижняя 303
График функции у =f(x) 201
- z =f(x, у) 303 Группа 187
- абелева (коммутативная) 187
- аддитивная 187
- бесконечная 187
- вращений правильного многоугольника 193
- единичная 189
- конечная 187 - мультипликативная 187
- полная линейная 188
- преобразований множества 191
- линейных 199
- симметрии треугольника 193
- симметрическая и-ой степени 190
- событий полная 518
- унимодулярная 190
- циклическая порядка и 193
Д
Двойной интеграл 320
- в декартовых координатах 322
- в полярных координатах 327
- несобственный 345
Действия над линейными преобразованиями 170 Декартов лист 39
Декартовы прямоугольные координаты вектора 59 ---г точки 5, 15
Деление отрезка в данном отношении 20,61 Дефект линейного преобразования 163 Дивергенция векторного поля (расходимость) 476 Директриса параболы 29
- эллипса 26
Директрисы гиперболы 27 Дискриминант уравнения квадратного 142
- кубического 144 Дискриминантная линия 318 Дисперсия случайной величины 530 - г - выборочная 540
- Дг генеральная 539
---Эмпирическая (исправленная) 540
Дифференциал вектор-функции 255
- длины дуги кривой плоской 250 ----пространственной 250
- функции 228
- второго порядка 231
- и-го порядка 231
- нескольких переменных полный 307 ----частный 309
Дифференциалы высших порядков 231,310 Дифференциальные уравнения 431
- Бернулли 434
- обыкновенные 431
---второго порядка 439
-----линейные неоднородные с
Постоянными коэффициентами 443
------однородные с постоянными
Коэффициентами 442
---первого порядка 432
-----в полных дифференциалах 436 -----линейные 434
-----однородные 433
-----с разделяющимися
Переменными 432
---и-го порядка 446
----линейные 449
-----неоднородные с постоянными
Коэффициентами 451
-----однородные с постоянными
Коэффициентами 449
- с частными производными 460 ----первого порядка 461
- — второго порядка 463
------гиперболического типа 463
------параболического типа 463
------эллиптического типа 463
- математической физики 467 Дифференцирование 222
- изображения 581
- неявной функции 313
- оригинала 580
- сложной функции 313
- степенных рядов 410
- функции комплексной переменной 553 Длина векгора в координатах 60
- дуги линии плоской 296
---пространственной 296
Доверительная вероягаосгь (надежность) 542 Доверительные границы 542 Доверительный интервал 542
Евклидово пространство 157 Единица мннмая 128
Зависимость между матрицами одного и > того же преобразования в различных базисах 165
- между непрерывностью н дифференцируемостью функции 222
Задача Дирихле 470 - Коши 439,453,468
- для системы 453, 454
- смешанная 468
Задачи на наибольшие и наименьшие значения 248
- приводящие к дифференциальным уравнениям 437
Закон распределения случайной величины 526,533 Замена переменной в определенном интеграле 283 Замена переменных в двойном интеграле 327 -----несобственном 347
- в тройном интеграле 353 Значение api умета 200
- собственное вектора линейного преобразования 167
- матрицы 168
- тл-кратиое 168
- функции 200
- наибольшее (абсолютный максимум) 248
- наименьшее (абсолютный минимум) 248
- среднее 286
Изменение порядка интегрирования в двойном интеграле 323 Изоморфизм групп 194
- линейных пространств 153 Инвариантность формы первого дифференциала 231
Интеграл вероятностей 282
- дифференциального уравнения 432 ---общий 432, 439,447
---частный 447
- Дюамеля 586
- Лапласа 578
- неопределенный 259
- несобственный 286
- определенный 278
-.- с переменным верхним пределом 281
- от функции^) 557
- поверхностный 377
- второго рода 380
- первого рода 377
- повторный 322
- Пуассона 470
- собственный 286 Интегралы Френеля 282 Интегральный косинус 282
- логарифм 282
- синус 282
Интегрирование дифференциальных биномов 273
- уравнений с помощью рядов 511
- изображения 581
- иррациональных функций 272
- непосредственное 262 - оригинала 581
- по частям 265,283
-- рациональных дробей с квадратным трехчленом в знаменателе 269
— функций 270
— тригонометрических выражений 275 Интерполяционная формула Лагранжа 497
— Ньютона 501
Интерполяционный многочлен Лагранжа 497
— Ньютона 501 Исследование функций 246
Каноническое уравнение гиперболы 27
— окружности 25
— параболы 28
Канонические уравнения прямой 80
— сферы 72
— эллипса 25 Каппа 44 Кардиода 44
Касательная плоскость 317
— прямая 220 Катеноид 96
Квадратичная форма 174
— действительная 174
— вырожденная 174
— знакоопределенная 178
— каноническая 176 ---нормальная 176
— комплексная 174
— невырожденная 174
— неопределенная 178
— отрицательно-определенная 178
— положительно-определенная 177
— полуопределениая 178 Квадратриса 51
Классы сопряженных элементов 197 Ковариация случайных величин 532 Комплексная плоскость 130 Комплексные числа 128
— сопряженные 129 Композиция функций 202 Конические сечения 31 Конус вращения 91
— второго порядка 91 Конхоида 42
— гиперболической спирали 51 Координата точки на прямой 4 Координаты вектора единичного 71
— заданного двумя точками 61
— линейного пространства 154
- линейной комбинации векторов 61
- полярные 6
- обобщенные 329
- Произведения вектора иа число 61
- разности двух векторов 61
- середины отрезка 5,7, 62
- суммы двух векторов 61 - сферические 18
- обобщенные 355
- на плоскости 5
- в пространстве 154
- точки пересечения медиан треугольника 8
- n-мерного пространства 301 ---на плоскости 327
- цилиндрические 17
Корень алгебраического многочлена 139
---кратный 140
--- простой 140
-уравнения 130
- квадратного уравнения 142
- кубического уравнения 143
- квадратный из комплексного числа 131
- многочлена характеристического 166
- функции 232
Корин и-ой степени из единицы 135
---из комплексного числа 135
Косинус угла между векторами евклидова пространства 160 Косинусы направляющие 60 Коэффициент корреляции 532 Коэффициенты ряда степенного 412
- Фурье 422 Кривая Внвиани 339
- Гаусса (нормальная кривая) 535
- непрерывная в Е„ 302 Кривизна линии плоской 251
- пространственной 251 Криволинейный интеграл второго рода 367
- первого рода 363
—, условия независимости от пути интегрирования 371 Круг сходимости степенного ряда 428
Л
Лемниската Бернулли 41 Линейная зависимость векторов 69
---линейного пространства 152
- комбинация векторов 59,152
---нетривиальная 152
---тривиальная 152
- независимость векторов 70
---линейного пространства 152
Линнн координатные 327 Лнннн уровня 471
Линии свода 54
Максимум функции 241
- абсолютный 248
- локальный 242
- нескольких переменных 314 --нестрогий 241
- строгий 241
Математическое ожидание случайной величины 529 Матрица 99
- диагональная 100 - единичная 101
- квадратная 100
- вырожденная (особенная) 109
- невырожденная (неособенная) 109 --обратная 109
- симметрическая 100
- квадратичной формы 174
- квазитреугольная (ступенчатая, трапециевидная) 101
- линейного преобразования 164
- линейной системы основная 117 ---расширенная 117
- нулевая 100
-, приводимая к диагональному виду 169 - ортогональная 172 - противоположная 102 - системы векторов 155 - скалярная 100
- столбец (столбцевая) 100
- строка (строчная)100 - транспонированная 101 - треугольная 101 - унитарная 161 Матрицы равные 99
- перестановочные (коммутативные) 103
- подобные 165 Метод Гаусса 122
- Д'Аламбера (метод характеристик) 468
-Жордана 110
- интегрирования по частям 265,283
- итераций 495
- касательных (метод Ньютона) 494
- подстановки (замены переменной) 263
- Руиге-Кутга 515
- Фурье (разделение переменных) 466
- хорд 492
- Чебышева 496
- Эйлера 514 Минимум функции 241
- абсолютный 248
- локальный 242
- нескольких переменных 314 Минор базисный 121
- главный квадратичной формы 178
- матрицы 114
- элемента определителя 106 Многочлен от квадратной матрицы 104
- аннулирующий 104 - характеристический 166 Множество замкнутое 302
- ограниченное 302
- открытое 302
- связное 302
- точек «-мерного пространства 302 Множитель Лагранжа 316 Модуль векгора 55
- комплексного числа 132
Моменты инерции материальной поверхности 387
- пластинки 340 --тела 341, 358
- статические 340
- случайной величины начальные 532 ---центральные 533
Наибольший общий делитель многочленов 138 Направляющий вектор прямой 80 Непрерывность вектор-функцин 255
- функции комплексной переменной 547-548
- функции y=f(x) 214
- нескольких переменных 304 Неравенство Кошн-Буняковского 159 - треугольника 159
Норма вектора евклидова пространства 158
----в координатах 160
Нормаль к лннии 221 Нормаль к поверхности 317 Нормальный делитель 196 Нули функции fiz) 569
Область замкнутая 302 - двусвязная 548
- значений функции 200
- интегрирования 322
- односвязная 548
- определения функции 200,303
- сходимости функционального ряда 408 Объем совокупности 538
- выборочной 538
- генеральной 538
- тела вращения 298
- параллелепипеда 67
- треугольной пирамиды 68 Овалы Касснни 42
Однопараметрическое семейство лнннй, огибающая 318
- поверхностей, огибающая 319 Окрестность точки 203 Окружность 25
- кривизны 252 Октант 16 Оператор 200
- Гамильтона (оператор набла) 481
- Лапласа 482 - линейный 162
Операционное (операторное) равенство 578-579
Определитель (детерминант) - второго порядка 105
- Вронского 450
- линейной системы уравнений 119
- л-го порядка 107
- произведения матриц 108 - третьего порядка 107 Опыт (испытание) 518 Ордината 16
Орты 59
Остаток ряда 390
Остаточный член в форме Лагранжа 233
---Пеано 233
Ось абсцисс 15 - аппликат 15
- координатная 4
- полярная 6 - ординат 15
Отображение множества в множество 200
- на множество 200 Отрезок направленный 4 Оценка доверительности 543
- интеграла двойного 321
- определенного 285
- тройного 349
- интервальная 542
- несмещенная 543
- параметра 544
- смещенная 539
- состоятельная 539
- средней квадратической погрешности 545
- точечная 543
- - дисперсии 544
- точного значения измеряемой величины 543
- точности измерений 544
- эффективная 539
Парабола 28
Параболоид вращения 91
- гиперболический 92
- эллиптический 92 Параллельный перенос 14 Параметры Ламе 473 Первообразная 259
- для непрерывной функции 282 Пересечение линий 11 Период функции 202 Плотность распределения 527 Площадь криволинейной фигуры 292
- параллелограмма 66
- поверхности вращения 298 - треугольника 9,66 Поверхности второго порядка 91
- вращения 89
- второго порядка 91
- уровня (эквипотенциальные поверхности) 471
- цилиндрические 89 Поворот координатных осей 14 Подгруппа 189
- инвариантная (нормальный делитель) 196
- несобственная (тривиальная) 190
- собственная (истинная) 190 Подпространство линейного пространства 151 Подстановка 191
- Эйлера 265
Подынтегральное выражение 259 Показатель роста функции 578 Полюс 6
Последовательность 202
- монотонная 204
- ограниченная 203
- сверху 203
- снизу 203
- расходящаяся 203
- сходящаяся 203
- числовая 203
Поток векторного поля 476 Правила дифференцирования 223 Правило замыкающей 56
- Лопиталя-Бернулли 237
- параллелепипеда 57
- параллелограмма 56
- треугольника 56
- трех сигм 536, 544 Предел вектор-функции 254
- интегральной суммы 278
- интегрирования верхний 278
- нижний 278
- последовательности 202
- функции 205
- комплексной переменной 547
- нескольких переменных 303
- прн х —> 206
- односторонний 205
- слева 205 1
- справа 205
—J(x)=(siwc)/x прн х—>0211 Представления групп 199
- линейные 199
Преобразование взаимно однозначное (биективное)162
- квадратичной формы 175
- Лапласа 578
- линейного пространства 162
- линейное (линейный оператор) 162
- в координатах 164
- вырожденное 171
- невырожденное 171 --обратное 171
- - ортогональное 173
- переменных 190 --унитарное 162
- множества 190
Преобразование декартовых координат 14, 62
- координат вектора 156 Приближенное вычисление корней
Уравнения 491
- определенных интегралов 505 Приведение двойного интеграла к
Повторному 322 Признак Абеля 401
- Вейерштрасса 410
- возрастания функций 240 - Гаусса 398
- Д'Аламбера 398
- Дирихле 401
- интегральный 394
- Коши 398 - Лейбница 401
- полного дифференциала 372
- постоянства функций 240
- Раабе 398
- сравнения рядов второй 394 ---первый 394
- сходимости ряда необходимый 390
- убывания функций 240 Приложения двойных интегралов 330,341
- интегралов по поверхности 386
- криволинейных интегралов 373
- тройных интегралов 357 Приращение аргумента 214 - функции 214
- полное 304
- частное 304 Проекция вектора на ось 58
- точки на плоскость 87 Произведение вектора на число 58,61
- двух пар упорядоченных чисел 127
- комплексных чисел 130 - матриц 103
- матрицы на число 102
- преобразований 170
- ряда на число 404
- рядов 404
- событий (пересечение) 519
- тензоров 486 Производная 220
- бесконечная 221
- вектор-функцин 255
- логарифмической функции 225
- неявной функции 226
- обратной функции 223
- односторонняя 221
- от матрицы 457
- показательной функции 225
- произведения функций 223
- слева 221
- сложной функции 223 - справа 221
- суммы (разности) функций 223
- функции, заданной параметрически 226
- функции комплексной переменной 553
- функции и" 226
- частная второго порядка 310 ----смешанная 310 —и-го порядка 311
- первого порядка 306
- частного двух функций 223 Производные высших порядков 227
- гиперболических функций 226
- обратных тригонометрических - функций 225
- степенных функций 224
- тригонометрических функций 224 Пространство^)
- арифметическое и-мерное 301
- вероятностное 521 - линейное (векторное) 150
- бесконечное 154
- действительное 150
- изоморфные 154
- комплексное 150
- конечномерное 153
- представления группы 199
- унитарное 161
- элементарных событий 520 Простое отношение трех точек 5 Прямая как пересечение двух плоскостей 85 Прямая на плоскости 19
- в пространстве 80 Прямолинейные образующие поверхности 94
- гиперболический параболоида 94
- однополостного гиперболоида 94 Пучок плоскостей 86 Псевдосфера 98
Р
Работа переменной силы 374 Радиус-вектор 59 Радиус кривизны 252
- полярный 6
- сходимости степенного ряда 413,428 Разложение вектора по двум
Неколлинеарным векторам 69
- по трем некомпланарным векторам 60,69
- группы по подгруппе 195
- определителя по элементам строки (столбца) 107
- элемента линейного пространства по базису 154
Размерность линейного пространства 153 Разности разделенные 499
- различных порядков 499
Разность векторов 57
- даух матриц 102
- пар упорядоченных чисел 127
- рядов 404
- событий 519
Ранг квадратичной формы 174
- линейного преобразования 163 - матрицы 114
- системы векторов линейного пространства 155 Раскрытие неопределенностей 237 Распределение вероятностей случайной
Величины 526
- биноминальное 533
- геометрическое 533
- нормальное (Гаусса) 535
- показательное 534'
- Пуассона 533
- равномерное 534 Расстояние между двумя точками в
Пространстве 16
----«-мерном пространстве 301
----на плоскости 7
- от точки до прямой 23,84 ---до плоскости 82
- между даумя прямыми 84 Решение дифференциального уравнения
Обыкновенного 432
----общее 432,439,447
----особое 447
----частное 432,439,447
---с частными производными 460
Роза 45
- трехлепестковая 46
- четырехлепестковая 45
Ротор векторного поля (вихрь) 478 Ряд Лорана 564
- Тейлора 563 Ряд числовой 389
- абсолютно сходящийся 400
- гармонический 390
- геометрический 390
- гипергеомегрический 399
- Дирихле 396 ,
- знакопеременный 400
- знакочередующийся 400
- мажорантный 410
- неабсолютно (условно) сходящийся 400
- расходящийся 389
- сходящийся 389
- функциональный 389
— биномиальный 421
— степенной 412
---в комплексной области 427
---Маклорена 418
---Тейлора417
— сходящийся абсолютно 408 ---равномерно 410
— Фурье 422
---для функций, заданный на отрезке
(-/,0423 ---в комплексной форме 423
С
Свертка функций 585 Свертывание тензора 486 Семейства линий 318
— поверхностей 318
Сигнатура квадратичной формы 177 Симметрирование тензоров 487 Система векторов ортогональная 160
— ортонормированная 160
— координат полярная 6
— левая и правая 15,65
— линейных алгебраических уравнений 116
— дифференциальных уравнений с постоянными коэффициентами 453
Скалярное поле 471
— - дифференцируемое 472
— осесимметрическое 471
— плоскопараллельное 471
— сферическое 471
— произведение двух векторов 62, 158
----в координатах 63
------в ортонормированием
Базисе 161 Скалярный квадрат вектора 63,158 Случайная величина 526
— дискретная 526
— непрерывная 527
Смешанное произведение трех векторов 67
----в координатах 68
Собственные векторы линейного преобразования 167 Событие 518, 519
— достоверное 518, 519
— невозможное 518, 519 - случайное518, 519 - элементарное 520 События независимые 523
— несовместные 518, 520
- противоположные 518, 520
- равновозможные 518
- совместные 518
Совокупность выборочная (выборка) 538
- генеральная 538 Спираль алгебраическая 50
- "жезл" 51
- Архимеда 49
- Галилея 51
- логарифмическая 51
- параболическая 51 - Ферма 51
Способ неопределенных коэффициентов 443 Среднее квадратическое отклонение 531
---выборочное 540
---генеральное 539
---исправленное (эмпирический стандарт) 540
Статистическое распределение выборки 538 Строфоида 40 Сумма векторов 56
- двух пар упорядоченных чисел 127
- рядов 404
- интегральная 320,349,363,367,377
- комплексных чисел 130
- матриц 102 - преобразований 170
- ряда389
- частичная 389
- событий (объединение) 518
- тензоров 486 Суперпозиция функций 202 Сфера 72
- (и-1)-мерная 301 Схема Горнера 139
Таблица Кэ^и 192
- неопределенных интегралов 260
- основных дифференциалов 231 Тензор 485
- ковариантный 485
- контравариантный 485
- кососимметрический 488 Тензорное поле 489 Теорема Абеля 412 - аннулирования 107 - Безу 139
- Бейеса 525
- Бернулли 536
- Вейерштрасса 410 - замещения 107
- запаздывания S8S
- Коши 232, 558 - Крамера 119
- Кронекера-Капелли 121
- Кэли 199
- Лагранжа 196,232
- Ляпунова 536
- об устойчивости знака непрерывной функции 211,305
- о переходе к пределу в неравенстве 211
- о среднем 285
- Остроградского 477
- подобия 585
- разложения 586- 587
- Ролля 232
- смещения 585 - Стокса 479
- умножения (теорема Бореля) 585
- вероятностей 522
- Чебышева 536 Теоремы Лапласа 537
- о пределах 211 Тор 96
Точка внутренняя 302
- граничная 302
- изолированная 302 - касания 317
- и-мерного пространства 301
- особая 569
- изолированная 569
- полюс 570
- существенно 570
- устранимая 570
- перегиба 245
- предельная 302
- разрыва функции 217
---второго рода 217
---первого рода 217
- устранимого 217
- расходимости функционального ряда 408
- сходимости функционального ряда 408 - экстремума 314
Точность оценки 543 Трактриса 53
Транспонирование тензоров 487 Трансцендентная линия 49 Тригонометрическая форма комплекс - ' ного числа 133
Тройка векторов 64
- левая 64
- правая 64
Тройки одной ориентации 64
- различной ориентации 64 Тройной интеграл 349
- в сферических координатах 354
- в цилиндрических координатах 354
Угловой коэффициент прямой 19 Угол между векторами евклидова пространства 160 —двумя плоскостями 81 ---прямыми 21, 83
- прямой и плоскостью 86
- полярный 6
- смежности 251 Улитка Паскаля 44 Умножение поворотов 193 - подстановок 191 Упорядоченная пара чисел 127 Уравнение(я)
- алгебраическое второй степени относительно хиу 19
- первой степени относительно хиу 19
- биссектрис углов между прямыми 23
- векторного движения точки 253
- касательной прямой 221,257
- плоскости 318
- квадратное 142
- координатных осей 73
- плоскостей 72
- кубическое 143
- линии на плоскости 10
----в декартовых координатах 10
----в полярных координатах 12
----параметрические 13
- в пространстве 72 ----параметрические 73
- нормали к линии 221
- к поверхности 318
- нормальной плоскости 257
- окружности 25
- плоскости (различные виды) 75-78
- поверхности 72
- вращения 91
---параметрические 96
- параметрические 73
- полярное гиперболы, параболы, эллипса 30
- прямой в пространстве (различные виды) 80
- на плоскости (различные виды) 19
- четвертой степени 145
Условия Д'Аламбера-Эйлера (Коши-Римана) 553
- коллинеарности двух векторов 58,61,65
- компланарности трех векторов 67,68
- линейной зависимости векторов 69
- ортогональности двух векторов 160
- параллельности двух прямых 21, 83
- перпендикулярности двух векторов 63 ---прямых 21, 83
- экстремума достаточное 243
- необходимое 242
Фактор-группа 197
Фигура второго порядка гиперболического типа на плоскости 181
---в пространстве 183
---на плоскости 180
---нецентральная в пространстве 184
----на плоскости 181
---центральная в пространстве 184
----на плоскости 181
---эллиптического типа на плоскости 181
Фокальный параметр 30 Формула Бейеса 525
- Бернулли 533 - Грина 371
- Д'Аламбера 469
- Кардано 144
- Коши интегральная 561
- Маклорена 233
- Муавра 135
- Ньютона-Лейбница 281
- Остроградского 384
- парабол (формула Симпсона) 507
- полной вероятности 525
- Стокса 384 - Тейлора 233,311
- трапеций 506 Формулы Виета 140 - дифференцирования 224
- Крамера 119
- преобразования координат 14, 62, 156
- приближенные 235
- прямоугольников 505 - Эйлера428, 550
Функция 200
- аналитическая 554
- бесконечно большая 210
- малая'207
- возрастающая 240
- гармоническая 470, 554
- двух переменных 303 - дифференцируемая 221,229,308, 553
- дробная рациональная 147
- изображение 578 .
- интегральная показательная 282
- интегрируемая 279, 321
- комплексной переменной 547 ---многозначная 548
---однозначная 547
-Лагранжа 316
- Лапласа 535
- непрерывная в точке 214
- на интервале 215
- на отрезке 215
- нескольких переменных 303
- нечетная 202
- неявная 201, 304,313
- обратная 201
- ограниченная 202
- однородная 433
- оригинал 578
- сложная (от функции) 202,313
- первообразная 259
- периодическая 202
- подынтегральная 259
- показательная (экспоненциальная) 218
- полилинейная 483
- распределения случайной величины 527
- эмпирическая 539
- трех переменных 304
- убывающая 240
- Хевисайда 578
- целая рациональная 147
- четная 202
- числовая 200
- явная 201,304
Функции гиперболические 218
- комплексной переменной 550
- линейно-зависимые 450
- линейно-независимые 450
- нескольких переменных 303
- элементарные комплексной переменной 549
Характеристики уравнения с частными производными 463 Характеристический многочлен линейного преобразования 166 Характеристическое уравнение линейного преобразования 165
— для дифференциального уравнения 442,449,463
Характеристические числа линейного преобразования 165
Ц
Целая положительная степень матрицы 104 Центр кривизны 252
- тяжести материальной дуги 374 ---поверхности 386
— пластинки 340
— системы масс 9
— тела 341,358
- распределения 529 Цепная линия 55 Циклоида 13
- удлиненная 50
- укороченная 50 Цилиндр гиперболический 92
- параболический 92
- эллиптический 92 Циркуляция векторного поля 478 Циссоида 39
Частная производная функции нескольких переменных 305 Частное двух пар упорядоченных чисел 127 Частные производные высших порядков 310 Частота события 520
— относительная 520
— условная 520
- варианты 538
— относительная 538
Числовые характеристики случайных величин 532
Число е 212
- мнимое 128
Шар л-мерный замкнутый 301
- открытый 301
Эвольвента 252 Эволюта 252
Экстремум функции y=f(x) 241
- нескольких переменных 314 - условный 316 Эксцентриситет гиперболы 27
- эллипса 25 Эпемент(ы) группы 187
- нейтральный 187 - обратный 187
- сопряженные 197
- линейного пространства (вектор) 150 ---нормированный 160
---нулевой 150
---противоположный 150
- матрицы 99
- определителя 106
- последовательности 203 Элементарные дроби 148
' - преобразования матриц 102
- линейной системы уравнений 117
- функции 202
- основные 202 Эллипс 25
- вершины 32
- параметрические уравнения 31
- уравнение, отнесенное к вершине 31 Эллипсоид 91
- вращения 90 Эмпирические формулы 545 Эпитрохоида 48 Эпициклоида 48
Я
Якобиан (функциональный определитель) 327,353
Предисловие I АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Глава 1. Координаты на прямой, на плоскости, в пространстве 4
1.1. Координаты на прямой 4
1.2. Координаты на плоскости 5 .
1.3. Расстояние между двумя точками 7
1.4. Деление отрезка в данном отношении 7
1.5. Центр тяжести системы масс 9
1.6. Площадь треугольника 9
1.7. Уравнение линии в декартовых координатах 10
1.8. Пересечение линий 11
1.9. Уравнение линии в полярных координатах 12
1.10. Параметрические уравнения линии 13
1.11. Преобразования декартовых 14
1.12. Прямоугольные декартовы координаты в пространстве 15
1.13. Расстояние между двумя точками в пространстве 16
1.14. Цилиндрические и сферические координаты 17
Глава 2. Линии на плоскости 19
2.1. Прямая на плоскости 19
2.2. Окружность 25
2.3. Эллипс 25
2.4. Гипербола 27
2.5. Парабола 28
2.6. Полярное уравнение эллипса, гиперболы, параболы 29
2.7. Некоторые другие виды уравнений линий второго порядка 31
2.8. Упрощение уравнения второй степени, не содержащего члена с произведением координат 33
2.9. Упрощение общего уравнения второй степени 35
2.10. Некоторые алгебраические линии высших порядков 39
2.11. Некоторые трансцендентные линии 49
3.1. Основные понятия 55
3.2. Линейные операции над векторами 56
3.3. Проекция вектора на ось 58
3.4. Декартовы прямоугольные координаты вектора в пространстве. Длина вектора. Направляющие косинусы вектора 59
3.5. Переход от векторных соотношений к координатным 61
3.6. Скалярное произведение двух векторов 62
3.7. Правые и левые тройки векторов. Правые и левые системы координат 64
3.8. Векторное произведение двух векторов 65
3.9. Смешанное произведение трех векторов 67
3.10. Линейная зависимость векторов 69
3.11. Аффинные координаты 70
Глава 4. Поверхности и линии в пространстве 72
4.1. Уравнение поверхности. Уравнения линии в пространстве 72
4.2. Параметрические уравнения линии и поверхности 73
4.3. Различные виды уравнения плоскости 75
4.4. Различные виды уравнений прямой в пространстве 80
4.5. Задачи, относящиеся к плоскостям 81
4.6. Задачи, относящиеся к прямым в пространстве 83
4.7. Задачи на прямую и плоскость 85
4.8. Цилиндрические поверхности. Поверхности вращения 89
4.9. Поверхности второго порядка 91
4.10. Некоторые другие поверхности 96
II АЛГЕБРА 99 Глава 5. Матрицы и определители 99
5.1. Матрицы. Основные определения 99
5.2. Линейные действия над матрицами 102
5.3. Произведение матриц. Многочлены от матриц 103
5.4. Определители и их свойства 105
5.5. Обратная матрица 109
5.6. Ранг матрицы 114
6.1. Линейные системы. Основные определения 116
6.2. Матричная запись линейной системы 117
6.3. Невырожденные линейные системы 119
6.4. Произвольные линейные системы 121
6.5. Метод Гаусса 122
127
7.1. Упорядоченные пары действительных' чисел и операции над ними 127
7.2. Понятие комплексного числа. Алгебраическая форма комплексного числа 128
7.3. Геометрическое изображение комплексных чисел 129
7.4. Действия над комплексными числами 130
7.5. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа 132
7.6. Действия над комплексными числами, заданными в тригонометрической форме 134
Глава 8. Алгебраические уравнения
137
8.1. Алгебраические многочлены 137
8.2. Корни многочлена. Теорема Безу 139
8.3. Квадратные уравнения 142
8.4. Кубические уравнения 143
8.5. Уравнения четвертой степени 145
8.6. Решение алгебраических уравнений способом разложения многочлена 146
8.7. Разложение дробной рациональной функции в сумму элементарных дробей 147
Глава 9. Линейные пространства
150
9.1. Линейное пространство. Подпространство 150
9.2. Линейная зависимость и линейная независимость векторов линейного пространства 152
9.3. Размерность и базис линейного пространства. Изоморфизм линейных пространств 153
9.4. Координаты вектора линейного пространства 154
9.5. Ранг системы векторов линейного пространства 155
9.6. Преобразование координат вектора при изменении базиса 156
9.7. Евклидово пространство 157
9.8. Унитарное пространство 161
Глава 10. Линейные преобразования (линейные операторы) I62
10.1. Линейное преобразование и его матрица 162
10.2. Линейное преобразование в координатах 164
10.3. Зависимость между матрицами одного и того же преобразования в различных базисах. Подобные матрицы 165
10.4. Характеристическое уравнение линейного преобразования 165
10.5. Собственные векторы линейного преобразования 167
10.6. Приведение матрицы линейного преобразования к диагональному виду 169
10.7. Действия над линейными преобразованиями 170
10.8. Невырожденные линейные преобразования. Преобразование, обратное данному 171
10.9. Ортогональные матрицы 172
10.10. Ортогональные преобразования 173
Глава 11. Квадратичные формы 174
11.1. Квадратичная форма и ее матрица 174
11.2. Преобразование квадратичной формы при линейном однородном преобразовании переменных 175
11.3. Приведение действительной квадратичной формы к нормальному виду 176
11.4. Закон инерции квадратичных форм 177
11.5. Знакоопределенные квадратичные формы 177
11.6. Приведение квадратичной формы к каноническому виду ортогональным преобразованием переменных 178
11.7. Упрощение уравнений фигур второго порядка на плоскости 180
11.8. Упрощение уравнений фигур второго порядка в пространстве 183
12.1. Понятие группы. Основные определения 187
12.2. Примеры групп 188
12.3. Подгруппа 189
12.4. Группы преобразований. Симметрическая группа и-й степени 190
12.5. Группа вращений правильного многоугольника. Циклические группы. Группа симметрий правильного треугольника 193
12.6. Изоморфизм групп 194
12.7. Разложение группы по подгруппе 195
12.8. Нормальный делитель 196
12.9. Классы сопряженных элементов 196
12.10. Фактор-группа 197
12.11. Гомоморфизм групп 198
12.12. Представления групп 199
III МАТЕМАТИЧЕСКИЙ АНАЛИЗ 200 Глава 13. Функции и пределы 200
13.1. Понятие функции. Основные определения 200
13.2. Предел последовательности 202
13.3. Предел функции 205
13.4. Бесконечно малые функции и их свойства 207
13.5. Сравнение бесконечно малых функций 208
13.6. Бесконечно большие функции 210
13.7. Основные теоремы о пределах функций 211
13.8. Некоторые важные пределы 211
13.9. Непрерывность функции 214
13.10. Точки разрыва функции 216
13.11. Показательная функция. Гиперболические функции 218
Глава 14. Производные и дифференциалы 220
14.1. Понятие производной, ее геометрический и физический смысл 220
14.2. Основные правила дифференцирования 223
14.3. Основные формулы дифференцирования 224
14.4. Дифференциал функции 228
14.5. Основные теоремы дифференциального исчисления 232
14.6. Формула Тейлора 233
14.7. Формула Тейлора для некоторых функций 234
14.8. Приближенные формулы 235
Глава 15- Приложения Производной 237
15.1. Правило Лопиталя-Бернулли 237
15.2. Признаки постоянства, возрастания и убывания функции 240
15.3. Экстремум функции 241
15.4. Направления выпуклости, точки перегиба 244
15.5. Асимптоты 245
15.6. Исследование функций и построение их графиков 246
15.7. Задачи на наибольшие и наименьшие значения 248
15.8. Дифференциал длины дуги кривой 249
15.9. Кривизна плоской кривой 250
15.10. Окружность кривизны. Центр и радиус кривизны. Эволюта и эвольвента 252
15.11. Переменная векторная величина. Вектор-функция скалярного аргумента 252
15.12. Дифференцирование вектор-функций 254
15.13. Уравнения касательной к пространственной линии. Кривизна пространственной линии 256
Глава 16. Неопределенный интеграл 259
16.1. Неопределенный интеграл и его свойства. Таблица основных неопределенных интегралов 259
16.2. Непосредственное интегрирование 262
16.3. Метод подстановки 263
16.4. Метод интегрирования по частям 265
16.5. Интегрирование рациональных дробей с квадратным трехчленом в знаменателе 269
16.6. Интегрирование рациональных функций 270
16.7. Интегрирование простейших иррациональных функций 272
16.8. Интегрирование некоторых тригонометрических выражений 275
Глава 17. Определенный интеграл 278
17.1. Определенный интеграл, его геометрический смысл и свойства 278
17.2. Определенный интеграл с переменным верхним пределом. Формула Ньютона - Лейбница 281
17.3. Замена переменной в определенном интеграле.
Интегрирование по частям 283
17.4. Оценка определенного интеграла. Теорема о среднем 285
17.5. Несобственные интегралы 286
17.6. Интегралы Эйлера 290
17.7. Площадь криволинейной фигуры 292
17.8. Длина дуги кривой 296
17.9. Объем тела. Площадь поверхности вращения 298
Глава 18. Дифференциальное исчисление функций нескольких переменных 301
18.1. Множества в и-мерном пространстве 301
18.2. Понятие функций нескольких переменных 303
18.3. Предел и непрерывность функций нескольких переменных 304
18.4. Частные производные функции нескольких переменных 305
18.5. Полный дифференциал функции нескольких переменных 307
18.6. Частные производные и дифференциалы высших порядков. Формула Тейлора 310
18.7. Дифференцирование неявных и сложных функций 313
18.8. Экстремум функции нескольких переменных 314
18.9. Условный экстремум 316
18.10. Касательная плоскость и нормаль к поверхности 317
18.11. Семейства линий и их огибающие. Семейства поверхностей и их огибающие 318
Глава 19. Двойной интеграл 320
19.1. Понятие двойного интеграла, его геометрический и механический смысл 320
19.2. Вычисление двойного интеграла в декартовых прямоугольных координатах 322
19.3. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах 326
19.4. Вычисление площадей плоских областей 330
19.5. Вычисление объемов тел 332
19.6. Вычисление площадей поверхностей 336
19.7. Приложения двойных интегралов в механике 340 1-9.8. Несобственные двойные интегралы 344
Глава 20. Тройной интеграл 349
20.1. Понятие тройного интеграла. Оценка тройного интеграла 349
20.2. Вычисление тройного интеграла в декартовых прямоугольных координатах 350
20.3. Замена переменных в тройном интеграле 353
20.4. Приложения тройных интегралов 357
Глава 21. Криволинейные интегралы 363
21.1. Криволинейные интегралы первого рода 363
21.2. Криволинейные интегралы второго рода 367
21.3. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования 371
21.4. Приложения криволинейных интегралов 373
Глава 22. Интегралы по поверхности 377
22.1. Поверхностные интегралы первого рода 377
22.2. Поверхностные интегралы второго рода 380
22.3. Формула Стокса. Формула Остроградского 384
22.4. Приложения интегралов по поверхности 386
23.1. Основные понятия. Необходимый признак сходимости 389
23.2. Ряды с положительными членами. Признаки сходимости. Признаки сравнения. Интегральный признак Коши 394
23.3. Признак Д’Аламбера. Признак Коши. Другие признаки 397
23.4. Знакопеременные ряды 400
23.5. Действия над рядами 404
23.6. Некоторые числовые ряды и их суммы 405
Глава 24. Функциональные ряды 408
24.1. Сходимость функциональных рядов 408
24.2. Равномерная сходимость функциональных рядов 410
24.3. Степенные ряды. Действия над степенными рядами 412
24.4. Ряд Тейлора. Ряд Маклорена 417
24.5. Применения рядов в приближенных вычислениях 421
24.6. Ряды Фурье 422
24.7. Степенные ряды с комплексной переменной 427
IV ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 431 Гпава 25. Дифференциальные уравнения первого порядка 432
25.1. Уравнение с разделяющимися переменными 432
25.2. Однородные уравнения 433
25.3. Линейные уравнения. Уравнение Бернулли 434
25.4. Уравнения в полных дифференциалах 436
25.5. Задачи, приводящие к дифференциальным уравнениям 437
Глава 26: Дифференциальные уравнения второго порядка 439
26.1. Простейшие дифференциальные уравнения второго порядка. Случаи понижения порядка 439
26.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами 442
26.3. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 443
Глава 27. Дифференциальные уравнения высших порядков. Системы дифференциальных уравнений 446
27.1. Основные понятия 446
27.2. Простейшие интегрируемые дифференциальные уравнения высших порядков 447
27.3. Линейные однородные уравнения и-го порядка с постоянными коэффициентами 449
27.4. Линейные неоднородные уравнения и-го порядка с постоянными коэффициентами 451
27.5. Системы линейных дифференциальных уравнений с постоянными коэффициентами 453
27.6. Нормальные системы дифференциальных уравнений 454
27.7. Применение матриц к решению систем дифференциальных уравнений с постоянными коэффициентами 457
Глава 28. Дифференциальные уравнения с частными
460
28.1. Основные определения 460
28.2. Линейные дифференциальные уравнения с частными производными первого порядка 461
28.3. Линейные дифференциальные уравнения с частными производными второго порядка 463
28.4. Основные дифференциальные уравнения математической физики 467
Глава 29. Элементы векторного и тензорного анализа
471
29.1. Скалярное поле. Поверхности и линии уровня скалярного поля 471
29.2. Градиент скалярного поля. Производная по направлению 472
29.3. Векторное поле. Векторные линии 475
29.4. Поток векторного поля через поверхность. Дивергенция. Соленоидальное поле. Теорема Остроградского 476
29.5. Циркуляция векторного поля 478
29.6. Ротор векторного поля. Теорема Стокса 478
29.7. Потенциальное поле 480
29.8. Оператор Гамильтона. Операции второго порядка в векторном анализе. Оператор Лапласа 481
29.9. Полилинейные функции векторного аргумента. Понятие тензора 483
29.10. Действия над тензорами 486
29.11. Тензоры в евклидовом пространстве 488
29.12. Тензорное поле 489
/
491
491
Глава 30. Приближенное решение уравнений
30.1. Отделение корней уравнения 491
30.2. Метод хорд 492
30.3. Метод касательных 494
30.4. Метод итераций 495
30.5. Метод Чебышева 496
Глава 31. Интерполирование функций 497
31.1. Интерполяционный многочлен Лагранжа 497
31.2. Разности различных порядков. Разделенные разности 499
31.3. Интерполяционный многочлен Ньютона 501
Глава 32. Приближенное вычисление определенных интегралов 505
32.1. Формулы прямоугольников 505
32.2. Формула трапеций 506
32.3. Формула парабол 507
32.4. Приближенное вычисление определенных интегралов с помощью рядов 509
Глава 33. Приближенное решение дифференциальных уравнений 511
33.1. Интегрирование дифференциальных уравнений с помощью рядов 511
33.2. Метод Эйлера 514
33.3. Метод Рунге - Кутта 515
VI ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ 518
Глава 34. Случайные события и их вероятности 518
34.1. Классификация событий 518
34.2. Действия над событиями. Соотношения между событиями 518
34.3. Различные определения вероятности события 519
34.4. Условная вероятность. Теорема умножения вероятностей. Независимость событий 522
34.5. Формула полной вероятности. Формулы Бейеса 525
Глава 35. Случайные величины, их распределения и числовые характеристики 526
35.1. Дискретные случайные величины 526
35.2. Функция распределения. Плотность распределения 527
35.3. Математическое ожидание случайной величины 529
35.4. Дисперсия случайной величины 530
35.5. Некоторые другие числовые характеристики 532
35.6. Некоторые законы распределения случайных величин 533
35.7. Основные теоремы теории вероятностей 536
Глава 36. Элементы математической статистики и математической обработки результатов измерений 538
36.1. Основные понятия математической статистики 538
36.2. Доверительный интервал. Доверительная вероятность 542
36.3. Оценка точного значения измеряемой величины 543
36.4. Оценки точности измерений 544
36.5. Эмпирические формулы 545
УП ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 547 Глава 37. Элементы теории функций комплексной переменной 547
37.1. Понятие функции комплексной переменной. Предел и непрерывность 547
37.2. Основные элементарные функции комплексной переменной 549
37.3. Дифференцирование функций комплексной переменной 553
37.4. Интегрирование функций комплексной переменной 556
37.5. Интегральная формула Коши 561
37.6. Ряд Тейлора. Ряд Лорана 563
37.7. Нули функции. Особые точки 569
37.8. Вычеты функций 573
Глава 38. Элементы операционного исчисления 578
38.1. Оригинал и изображение 578
38.2. Основные правила и формулы операционного исчисления 580
38.3. Основные теоремы операционного исчисления 585
38.4. Решение дифференциальных уравнений и их систем 589
Приложение. Некоторые оригиналы и их изображения 597
Некоторые математические знаки й даты их возникновения 599 Биографический словарь 601 Предметный указатель 615
Гусак Алексей Адамович Гусак Галина Максимовна Бричикова Елена Алексеевна
Справочник по высшей математике
Главный редактор А. Ф.Мясников.
Редактор С. В.Процко.
Дизайн обложки С. А.Демидовой и Н. Б.Борковского.
Подписано в печать 22.12.98. - Формат 60x84 1/16. Бумага для офсетной печати. Гарнитура Таймс. Печать офсетная. Печ. л. 40. Усл. печ. л. 67.2. Тираж 5000 экз.
Заказ 1.
НТООО “ТетраСистемс” (Лицензия J1B № 76 от 19.11.97 до 19.11.2002). 220036, Минск, пер. Домашевский, 11А-508.
При участии ООО "НТЦ АПИ” (Лицензия ЛВ № 52 от 22.10.97 до 22.10.2002). 220102, Минск, ул. Социалистическая, 9-102.-
Качество печати соответствует качеству представленных издателем диапозитивов.
Отпечатано с готовых диапозитивов заказчика в типографии издательства “Белорусский Дом печати”. 220013, Минск, пр. Ф.Скорины, 79.
В случае правой тройки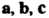
Векторы.
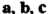. располагаются так, как большой, указательный и средний пальцы правой руки; если тройка
Является левой, то векторы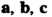
располагаются так, как указанные пальцы левой руки.
| < Предыдущая | Следующая > |
|---|
