10. Приложение 1. Главные значения расходящихся несобственных интегралов

К несобственным интегралам относятся так называемые интегралы в смысле главного значения. Если несобственный интеграл существует (сходится), то существует и интеграл в смысле главного значения и эти интегралы совпадают. Из существования интеграла в смысле главного значения не следует существование (сходность) соответствующего несобственного интеграла. Рассмотрим подробнее главные значения расходящихся несобственных интегралов по бесконечному промежутку и от разрывных функций.

Пусть функция f (x) определена на всей числовой оси и интегрируема на любом отрезке этой оси. Если существует предел:

1. ,

То он называется главным значением несобственного интеграла по бесконечному промежутку от функции f (x) и обозначается символом: , где V и P есть начальные буквы французских слов "Valeur Principal", обозначающих "главное значение". Итак, имеем по определению

2. .

В случае неотрицательной функции f (x) главное значение несобственного интеграла по бесконечному промежутку отождествляется с площадью неограниченной области между осью абсцисс и графиком этой функции.

Интеграл от нечетной функции fh (x) (fh (-x)= - fh (x)) по любому симметричному относительно начала координат отрезку [-R; R] равен нулю. По этой причине и главное значение несобственного интеграла по бесконечному промежутку от такой функции принимается равным нулю, то есть:

3. ,

Где fh (x) есть функция нечетная.

Например, , в то время как несобственный интеграл есть расходящийся; в самом деле: , то есть оба предела бесконечны; стало быть и сам несобственный интеграл расходится.

Аналогично равны нулю главные значения следующих расходящихся несобственных интегралов от нечетных функций по бесконечному промежутку: ; ; .

Интеграл от четной функции fr (x) (fr (x)= fr (-x)) по любому симметричному относительно начала координат отрезку [-R; R] равен удвоенному значению интеграла от этой функции на отрезке [0; R]. Главное значение несобственного интеграла по бесконечному промежутку от четной функции fr (x) существует, если несобственный интеграл от этой функции по промежутку [0; +) сходится. Таким образом, имеем:

4. ,

Где fr (x) есть функция четная.

Например, , в то время как несобственный интеграл расходится; в самом деле:

, где интегралы j2 и j4 есть расходящиеся, а потому и исходный интеграл расходится.

Главные значения несобственных интегралов по бесконечному промежутку от следующих четных функций: ; ; - не существуют, ибо расходятся соответствующие несобственные интегралы от этих функций; в самом деле: ; ; , ; xdx= =dv, , где безынтегральный член и предпоследний интеграл расходятся; стало быть и исходный интеграл расходится.

Упражнения: А) ; б) .

Известно, что сумма, разность и произведение четных функций есть функция тоже четная; сумма и разность нечетных функций есть функция нечетная, а произведение четного числа нечетных функций есть функция четная, в то время как произведение нечетного числа нечетных функций есть функция нечетная. Области определений четной и нечетной функций симметричны относительно начала координат. Любую функцию общего вида (ни четную, ни нечетную), определенную на симметричном относительно начала координат интервале, можно представить в виде суммы двух функций: четной (fr (x)) и нечетной (fh (x)) c общей для всех трех функций областью определения, то есть:

5. f (x)= fr (x)+ fh (x).

Это представление единственно, что нетрудно показать: так как f (-x)= fr (-x)+ +fh (-x)= fr (x)- fh (x), то с учетом соотношения (5) имеем систему двух уравнений с двумя неизвестными fr (x) и fh (x): из которой выражения для функций: четной fr (x) и нечетной fh (x),- определяется однозначно, а именно:

6а. ,

6б. .

Например, представим функцию общего вида в виде суммы функций четной fr (x) и нечетной fh (x): согласно формул (6а) и (6б) имеем: ; ; что верно, ибо: .

Понятие главного значения можно применить и к несобственным интегралам от разрывных функций, если особая точка, в которой имеет место разрыв функции, находится внутри отрезка интегрирования. Пусть функция f (x) интегрируема на промежутках: (a; с-ε] и [с+ε; b), ε> 0,- и неограниченна в окрестности точки ; тогда интегралом в смысле главного значения несобственного интеграла от разрывной функции называется предел:

7. .

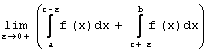Этот предел обозначается так: . Итак, имеем по определению:

8. ,

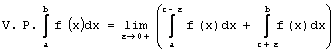Где f (c)= . Если существует несобственный интеграл от разрывной функции , то существует и интеграл в смысле главного значения, и эти интегралы равны. Из существования интеграла в смысле главного значения не следует существование соответствующего несобственного интеграла от разрывной функции.

Например, , в то время как несобственный интеграл не существует; в самом деле: , где оба интеграла расходятся.

Упражнения: А) ; б) .

Пример: .

Решение. В исследуемом интеграле две особые точки (x1= 1, x2= 2) и бесконечный промежуток интегрирования; поэтому разбиваем исходный интеграл на пять (!) интегралов, в каждом из которых будет только по одной особенности: . Последний интеграл сходится, а потому его величина равна главному значению этого интеграла, то есть . Далее найдем величину этого интеграла: . Остальные интегралы расходящиеся, а потому и исходный интеграл расходится. Посчитаем теперь главное значение расходящейся части интеграла, то есть: . Для этого разобьем интеграл на два интеграла, в каждом из которых особая точка будет находиться внутри соответствующего отрезка интегрирования: .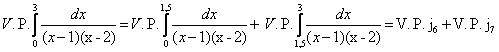

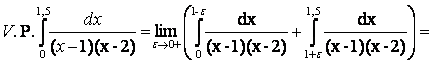
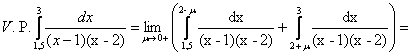
Далее ; 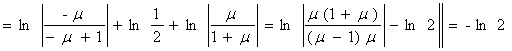. Итак, имеем: .

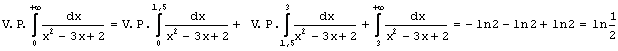Упражнения: А) б) .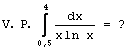

< Предыдущая