15. Свойства равномерно сходящихся рядов

1) Теорема о непрерывности суммы ряда.

Если члены ряда - непрерывные на отрезке [a, b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a, b].

2) Теорема о почленном интегрировании ряда.

Равномерно сходящийся на отрезке [a, b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т. е. ряд, составленный из интегралов от его членов по отрезку [a, b] , сходится к интегралу от суммы ряда по этому отрезку.

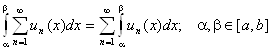
3) Теорема о почленном дифференцировании ряда.

Если члены ряда сходящегося на отрезке [a, b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных Сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.

На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.

На практике часто применяется разложение функций в степенной ряд

Теорема. (Признак равномерной сходимости Вейерштрасса)

(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)

Ряд Сходится равномерно и притом абсолютно на отрезке [a, b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :

Т. е. имеет место неравенство:

.

Еще говорят, что в этом случае функциональный ряд мажорируется числовым рядом

< Предыдущая		Следующая >