05. Признак сравнения рядов с неотрицательными членами

Пусть даны два ряда и при un, vn ³ 0.

Теорема. Если un £ vn при любом n, то из сходимости ряда Следует сходимость ряда , а из расходимости ряда Следует расходимость ряда .

Доказательство. Обозначим через Sn и sn частные суммы рядов и . Т. к. по условию теоремы ряд Сходится, то его частные суммы ограничены, т. е. при всех n sn < M, где М – некоторое число. Но т. к. un £ vn, то Sn £ sn то частные суммы ряда Тоже ограничены, а этого достаточно для сходимости.

Пример. Исследовать на сходимость ряд

Т. к. , а гармонический ряд расходится, то расходится и ряд .

Пример. Исследовать на сходимость ряд

Т. к. , а ряд сходится ( как убывающая геометрическая прогрессия), то ряд тоже сходится.

Также используется следующий признак сходимости:

Теорема. Если и существует предел , где h – число, отличное от нуля, то ряды и Ведут одинаково в смысле сходимости.

Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции.

Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее. (См. Формула Тейлора. )

Существует также способ разложения в степенной ряд при помощи алгебраического деления. Это – самый простой способ разложения, однако, пригоден он только для разложения в ряд алгебраических дробей

Рассмотрим способ разложения функции в ряд при помощи интегрирования.

С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной.

Находим дифференциал функции и интегрируем его в пределах от 0 до х.

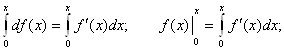
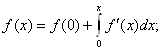
2) Теорема о почленном интегрировании ряда.

Равномерно сходящийся на отрезке [a, b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т. е. ряд, составленный из интегралов от его членов по отрезку [a, b] , сходится к интегралу от суммы ряда по этому отрезку.

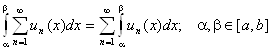
3) Теорема о почленном дифференцировании ряда.

Если члены ряда сходящегося на отрезке [a, b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных Сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.

На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.

На практике часто применяется разложение функций в степенной ряд.

< Предыдущая		Следующая >