03. Критерий Коши.(необходимые и достаточные условия сходимости ряда)

Для того, чтобы последовательность Была сходящейся, необходимо и достаточно, чтобы для любого существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:

.

1.3 Определение. Ряд Называется равномерно сходящимся на отрезке [a, b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.

Теорема. (Критерий Коши равномерной сходимости ряда)

Для равномерной сходимости ряда Необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство

Выполнялось бы для всех х на отрезке [a, b].

Теорема. (Признак равномерной сходимости Вейерштрасса)

(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)

Ряд Сходится равномерно и притом абсолютно на отрезке [a, b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :

Т. е. имеет место неравенство:

.

Еще говорят, что в этом случае функциональный ряд мажорируется числовым рядом .

Ряд называется положительным, если Un≥0, для всех n € N

Интегральный признак Коши.

Если j(х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j(1) + j(2) + …+ j(n) + … = и несобственный интеграл одинаковы в смысле сходимости.

Пример. Ряд сходится при a>1 и расходится a£1 т. к. соответствующий несобственный интеграл сходится при a>1 и расходится a£1. Ряд называется общегармоническим рядом.

Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b] и то интегралы и 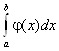ведут себя одинаково в смысле сходимости.

< Предыдущая		Следующая >