30. Решение систем дифференциальных уравнений

Последовательность действий для решения системы дифференциальных уравнений первого порядка такова (описана для значения ORIGIN=0):

Q перейти в исходной системе уравнений к однотипным обозначениям функций и выразить первые производные,

Например, систему 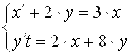можно преобразовать в ;

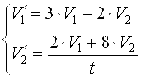Q в документе MathCad сформировать вектор начальных условий, количество элементов которого равно количеству уравнений системы, присвоив его некоторой переменной (см. тему 2);

например, ;

Q определить вектор-функцию, которая содержит первые производные искомых функций:

O набрать имя функции с двумя параметрами: первый параметр – аргумент искомых функций (независимая переменная), второй – имя вектора, содержащего искомые функции (можно использовать имя вектора начальных условий), например, D(T,V);

(Замечание: еСли независимая переменная явно не присутствует в системе, то в качестве ее имени можно выбрать любую переменную)

O набрать оператор «:=» и вставить шаблон вектора, количество элементов которого равно количеству уравнений системы (см. тему 2)

O набрать в качестве элементов вектора правые части системы уравнений, в которых искомые функции представлены соответствующими элементами вектора-параметра, например,

;

Q присвоить некоторой переменной значение функции Rkfixed, указав в скобках следующие параметры:

· первый – имя вектора начальных условий,

· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,

· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,

· четвертый – количество точек, в которых ищется решение,

· пятый – имя вектора-функции, описывающего первые производные, без параметров;

Например: ,

(в результате получится матрица Z, в первом столбце которой содержатся значения аргумента искомых функций, во втором – значения первой функции, в третьем – значения второй функции и т. д.);

Q вывести матрицу, содержащую решение системы ДУ с помощь оператора «=», например: Z = ;

Q построить графики найденных функций (см. тему 5), указав в качестве аргумента по оси абсцисс первый столбец матрицы решений, например, , а в качестве значений функций по оси ординат – остальные столбцы матрицы через запятую, например, , и т. д.

Пример 7.2 Найти решение системы дифференциальных уравнений

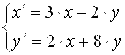
На интервале от 0 до 0.5 в 1000 точках, при следующих начальных условиях: x(0)=0.1 и y(0)=1.

Выполнить графическую интерпретацию результатов.

Реализация в MathCad:

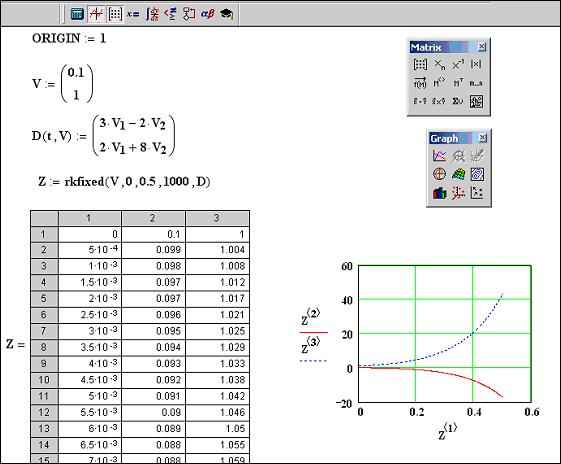
< Предыдущая		Следующая >