08. Тема 2. Обработка структурированных данных в MathCad. Краткие теоретические сведения

Дискретной называется переменная, содержащая несколько значений, изменяющихся от начального до конечного на величину постоянного шага. Дискретная переменная может быть задана двумя способами:

1) а := а1, а2 .. An

2) А := а1 .. An

Где A – имя дискретной переменной,

A1 – ее начальное значение,

A2 – ее второе значение,

An – ее конечное значение.

Символ «..» Набирается либо клавишей «;» на клавиатуре, либо кнопкой M..n – в палитре матриц.

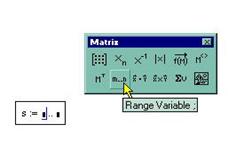
Для первого способа задания дискретной переменной шаг ее изменения равен (а2 – а1). Для второго способа задания дискретных переменных значение а2 не указывается, шаг изменения дискретной переменной равен 1, если a1<an, или -1, если a1>an.

Примеры создания дискретных переменных приведены ниже.

X:= 2.. 7	Создается дискретная переменная х, значения которой изменяются от 2 до 7 с шагом 1.
Y:= 2,2.3.. 7	Создается дискретная переменная y, значения которой изменяются от 2 до 7 с шагом 0.3.
Z:= 9 .. 1	Создается дискретная переменная z, значения которой изменяются от 9 до 1 с шагом -1.
A:= 8,7.9.. 3	Создается дискретная переменная a, значения которой изменяются от 8 до 3 с шагом -0.1.
	Создается дискретная переменная b, значения которой изменяются от 0 до 2π с шагом π/10.

Дискретные переменные могут являться аргументами функций, тогда процесс вычисления значений функции приобретает циклический характер, и для каждого значения дискретной переменной вычисляется свое значение функции по заданной аналитической зависимости.

В системе MathCAD в основном используются массивы двух типов: одномерные (векторы) и двумерные (матрицы).

Каждый элемент вектора или матрицы имеет порядковый номер в массиве. Отсчет номеров начинается с того значения, которое содержится в системной переменной ORIGIN. По умолчанию эта переменная имеет значение 0, для изменения значения нужно задать, например,

ORIGIN:=1

Векторы и матрицы можно задавать различными способами: с помощью кнопки с изображением матриц на наборной панели математических инструментов; как переменную с индексами перечислением элементов массива с разделение запятой; с помощью аналитического выражения.

Массивы могут использоваться в выражениях целиком или поэлементно. Для обращения к элементам массивов нужно указать числовые значения индексов элементов в подстрочнике после имени массива. При выполнении расчетов можно обращаться к конкретной строке или столбцу матрицы с помощью верхнего индекса или нижних индексов.

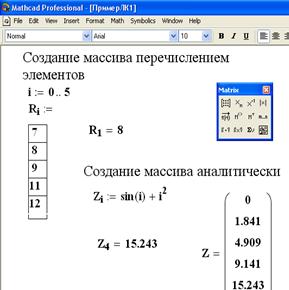
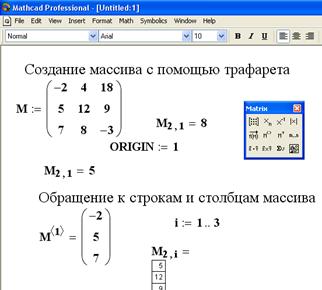
На рисунке 2.2.1 приведены примеры создания массивов перечислением элементов (вектор R) и аналитически (вектор Z). Здесь же показано, как обратиться к элементу матрицы, ее столбцу или строке. Из рисунка видно, что после изменения значения переменной ORIGIN, значение элемента матрицы M2,1 тоже изменяется.

Рисунок 2.2.1 – Примеры создания массивов

Существует ряд операций над матрицами и векторами, а также встроенных векторных и матричных функций. Введем следующие обозначения: V – вектор, M – матрица. Основные операции с их назначением и правилами набора приведены в таблице 2.2.1.

Таблица 2.2.1. – Основные операции и функции для обработки массивов

Вид операции	Назначение	Набор
|М|	Определитель матрицы
М-1	Обращение матрицы
МТ	Транспонирование матрицы
М< >	Выделение столбца матрицы
	Поэлементное умножение векторов
M∙V	Умножение матрицы на вектор	Знак умножения набирается с палитры арифметических операторов
М1·М2	Умножение двух матриц
V1∙V2	Умножение двух векторов
Max(M), min(M)	Максимум, минимум матрицы	Стандартные функции набираются с клавиатуры или с использованием мастера функций
Cols(M), rows(M)	Число столбцов и строк матрицы

< Предыдущая		Следующая >