16. Примеры решения задач 3
Пример 11.1. В январе 2014 года номинальный среднедушевой денежный доход составил 30 000 руб. За указанный период сводный индекс потребительских цен составил 1,11, а индекс реальных денежных доходов – 0,97. Рассчитать номинальный и реальный среднедушевой денежный доход в январе 2015 года по сравнению с январем 2014 года.
Согласно (11.2) индекс номинальных денежных доходов в январе 2015 года
Тогда номинальный денежный доход в январе 2015 года
Руб.
Реальный денежный доход в январе 2015 года согласно (11.1)
руб.
Таким образом, хотя номинальный доход увеличился на 2 301 руб., однако из-за роста цен реальный доход уменьшился 900 руб.
Пример 11.2. На основании данных о распределение населения по величине среднедушевых денежных доходов (в процентах) рассчитать: 1) средний доход; 2) модальный доход; 3) медианный доход; 4) коэффициент фондов (децильный); 5) децильный коэффициент дифференциации доходов населения; 6) коэффициент концентрации доходов Джини; 7) долю населения, имеющего доходы ниже среднего. Построить кривую Лоренца.
|
Номер группы |
Доходы, руб. |
Доля населения, % |
|
1 |
До 5 000,0 |
16,0 |
|
2 |
От 5 000,1 до 7 000,0 |
12,5 |
|
3 |
От 7 000,1 до 9 000,0 |
12,0 |
|
4 |
От 9 000,1 до 12 000,0 |
15,0 |
|
5 |
От 12 000,1 до 15 000,0 |
11,0 |
|
6 |
От 15 000,1 до 20 000,0 |
12,3 |
|
7 |
От 20 000,1 до 25 000,0 |
7,5 |
|
8 |
От 25 000,1 до 30 000,0 |
5,0 |
|
9 |
От 30 000,1 до 35 000,0 |
3,0 |
|
10 |
Свыше 35 000 |
5,7 |
В таблице ниже приведены промежуточные результаты расчетов. При проведении расчетов полагаем, что нижняя граница для 1-й группы равна 3 000, а верхняя граница для 10-й группы равна 40 000 руб.
1) Средний доход 
2) Модальный доход DMo. Так как в данном примере мы имеем интервальный ряд с неравными интервалами, поэтому для нахождения моды необходимо вместо частот (частостей) Fi использовать оценки плотности распределения вида 
.
Где XMo – нижняя граница модального интервала; HMo – величина модального интервала; 
– плотность распределения модального интервала; 
– плотность распределения интервала, предшествующего модальному; 
– плотность распределения интервала, следующего за модальным.
Для модального интервала оценка плотности распределения 
принимает наибольшее значение. В данном случае это 1-й интервал с плотностью 
. Тогда
3) Медианный доход DMe. Из-за того, что в этом примере используются неравные интервалы, формула для медианы имеет вид
,
Где XMe – нижняя граница медианного интервала; HMe – Величина медианного интервала; SMe-1 – член кумулятивного ряда частот (частостей), предшествующий медианному интервалу; FMe – частота (частость) медианного интервал.
Для определения медианного интервала воспользуемся кумулятивным рядом частостей Sxi, приведенным в таблице. Найдем, когда кумулятивный ряд Sxi в первый раз превысит половину общей суммы частостей 
. Это случится в 4-м интервале, т. к. выполнится неравенство 
. Таким образом, медианным интервалом оказался 4-й интервал. Тогда нижняя граница медианного интервала XMe=9 000; величина медианного интервала HMe=3 000; член кумулятивного ряда, предшествующий медианному интервалу SMe-1=S3=40,5; частость медианного интервала FMe=F4=15 и тогда
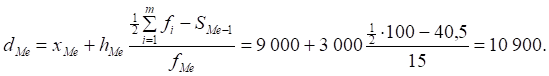
4) Коэффициент фондов (децильный) Kf.
В нашем примере 10% населения, имеющего минимальный доход, принадлежат 1-й группе, поэтому среднедушевой доход в месяц для них составляет 
руб.
10% самой богатой части населения относится к 10-й (5,7%), 9-й (3,0%) и 8-й группам (10–5,7–3,0=1,3%). Тогда средний уровень денежных доходов 10% населения с самыми высокими доходами:
Тогда коэффициент фондов
5) Децильный коэффициент дифференциации доходов населения. В случае неравных интервалов децили Dj рассчитывают по формуле
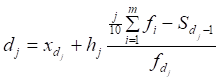, J=1,…, 9,
Где Xdj – нижняя граница интервала J-й децили; Hj – Величина интервала J-й децили; 
– член кумулятивного ряда, предшествующий интервалу J-й децили; 
– частота (частость) интервала J-й децили.
Для определения интервала 1-й децили найдем, когда кумулятивный ряд Sxi в первый раз превысит 1/10 общей суммы частостей 
. Это случится в 1-м интервале, т. к. выполнится неравенство 
. Таким образом, интервалом 1-й децили оказался 1-й интервал. Тогда нижняя граница интервала 1-й децили Xd1=3 000; величина интервала 1-й децили Hd1=2 000; член кумулятивного ряда, предшествующий интервалу 1-й децили Sd1-1=S0=0; частость интервала 1-й децили Fd1=F1=16 и тогда
Для определения интервала 9-й децили найдем, когда кумулятивный ряд Sxi в первый раз превысит 9/10 общей суммы частостей 
. Это случится в 8-м интервале, т. к. выполнится неравенство 
. Таким образом, интервалом 9-й децили оказался 8-й интервал. Тогда нижняя граница интервала 9-й децили Xd9=25 000; величина интервала 9-й децили Hd9=5 000; член кумулятивного ряда, предшествующий интервалу 9-й децили Sd9-1=S7=86,3; частость интервала 9-й децили Fd9=F8=5 и тогда
Тогда децильный коэффициент равен 
6) Коэффициент концентрации доходов Джини.
В таблице приведен пример расчета величин долей доходов Yi, сосредоточенных у I-й социальной группы, а также расчет кумулятивных (исчисленных нарастающим итогом) долей дохода i-й социальной группы S yi. Тогда согласно (11.5) индекс Джини равен
7) Доля населения, имеющего доходы ниже среднего.
В нашем случае средний доход 
Находим интервал, которому принадлежим это значение. Это пятый интервал – от 12 000,1 до 15 000,0. Тогда получаем
Здесь 0,551 – значение кумулятивной доли населения, соответствующей предшествующему интервалу (четвертому);12000 – нижняя граница пятого интервала; 3000 – величина пятого интервала (15000–12000); 0,11 – доля населения, соответствующая пятому интервалу. Таким образом, получаем, что 61,9% населения имеют доходы ниже среднего.
Для построения кривой Лоренца используют столбцы «Кумулятивная доля населения Sxi» (ось абсцисс) и «Кумулятивная доля доходов Syi» (ось ординат). Обратите внимание, что при построении кривой Лоренца необходимо добавить точку с координатами (0;0). График кривой Лоренца приведен на рис. 11.2.
|
Номер группы |
Доходы, руб. |
Доля |
Середина интервала Xi |
Xi×Fi |
Плотность распределения
|
|
1 |
До 5 000,0 |
16,0 |
4 000,0 |
640,0 |
16/2000=0,00800 |
|
2 |
От 5 000,1 до 7 000,0 |
12,5 |
6 000,0 |
750,0 |
12,5/2000=0,00625 |
|
3 |
От 7 000,1 до 9 000,0 |
12,0 |
8 000,0 |
960,0 |
12/2000=0,00600 |
|
4 |
От 9 000,1 до 12 000,0 |
15,0 |
10 500,0 |
1 575,0 |
15/3000=0,00500 |
|
5 |
От 12 000,1 до 15 000,0 |
11,0 |
13 500,0 |
1 485,0 |
11/3000=0,00367 |
|
6 |
От 15 000,1 до 20 000,0 |
12,3 |
17 500,0 |
2 152,5 |
12,3/5000=0,00246 |
|
7 |
От 20 000,1 до 25 000,0 |
7,5 |
22 500,0 |
1 687,5 |
7,5/5000=0,00150 |
|
8 |
От 25 000,1 до 30 000,0 |
5,0 |
27 500,0 |
1 375,0 |
5/5000=0,00100 |
|
9 |
От 30 000,1 до 35 000,0 |
3,0 |
32 500,0 |
975,0 |
3/5000=0,00060 |
|
10 |
Свыше 35 000 |
5,7 |
37 500,0 |
2 137,5 |
5,7/5000=0,00114 |
|
Итого |
100 |
13 737,5 |
Окончание таблицы
|
Номер |
Доля доходов
|
Кумулятивная доля |
Кумулятивная доля доходов |
Fi×Syi |
Fi×Yi |
|
1 |
4,7 |
16,0 |
4,7 |
0,0075 |
0,0075 |
|
2 |
5,5 |
28,5 |
10,1 |
0,0126 |
0,0068 |
|
3 |
7,0 |
40,5 |
17,1 |
0,0205 |
0,0084 |
|
4 |
11,5 |
55,5 |
28,6 |
0,0429 |
0,0172 |
|
5 |
10,8 |
66,5 |
39,4 |
0,0433 |
0,0119 |
|
6 |
15,7 |
78,8 |
55,1 |
0,0677 |
0,0193 |
|
7 |
12,3 |
86,3 |
67,3 |
0,0505 |
0,0092 |
|
8 |
10,0 |
91,3 |
77,3 |
0,0387 |
0,0050 |
|
9 |
7,1 |
94,3 |
84,4 |
0,0253 |
0,0021 |
|
10 |
15,6 |
100,0 |
100,0 |
0,0570 |
0,0089 |
|
Итого |
0,3660 |
0,0962 |
| ||
,%
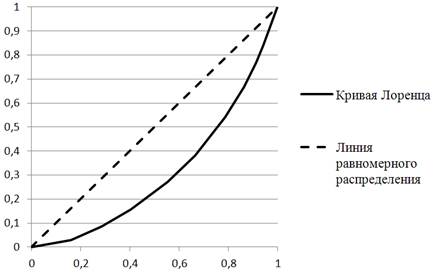
Рис. 11.2. График кривой Лоренца для примера 11.2
Пример 11.3.
Прожиточный минимум составляет для трудоспособного населения – 9 000 руб./мес., для пенсионеров – 6 000 руб./мес., для детей – 7 000 руб./мес. Рассчитайте коэффициент бедности, индекс глубины бедности и индекс остроты бедности на основании данных выборочного обследования. Оцените дефицит денежного дохода, если в городе на момент проведения обследования насчитывалось 20 тыс. домохозяйств.
Решение
Произведем расчет для первого домохозяйства.
Прожиточный минимум 1-го домохозяйства
PM1=2∙9 000+1∙6 000+2∙7000=38 000 руб.
Среднедушевая величина прожиточного минимума для 1-го домохозяйства (с учетом его половозрастной структуры)
руб./чел.
Среднедушевой доход 1-го домохозяйства
Руб./чел.
Так как среднедушевой доход 1-го домохозяйства превышает среднедушевую величину прожиточного минимума, поэтому дефицит денежного дохода в данном случае равен 0.
Для второго домохозяйства прожиточный минимум
PM2=2∙9 000+2∙6 000+1∙7000=37 000 руб.
Среднедушевой прожиточный минимум
руб./чел.
Среднедушевой доход
Руб./чел.
Дефицит денежного дохода
D2= PM2 – D2 = 37 000 – 20 000 = 17 000 руб.
В таблице ниже приведены результаты расчетов для остальных домохозяйств.
E Обратите внимание, что при расчете 
В таблицу заносятся только положительные значения!!!
|
№ |
Прожиточный минимум PMi, руб. |
Среднедушевой прожиточный минимум |
Среднедушевой доход |
Дефицит дохода Di, руб. |
|
|
1 |
38 000 |
7 600,00 |
8 000 |
0 |
0,000 |
|
2 |
37 000 |
7 400,00 |
4 000 |
17 000 |
0,459 |
|
3 |
67 000 |
7 444,44 |
8 889 |
0 |
0,000 |
|
4 |
13 000 |
6 500,00 |
17 500 |
0 |
0,000 |
|
5 |
29 000 |
7 250,00 |
11 250 |
0 |
0,000 |
|
6 |
41 000 |
8 200,00 |
7 200 |
5 000 |
0,122 |
|
7 |
39 000 |
7 800,00 |
5 000 |
14 000 |
0,359 |
|
8 |
22 000 |
7 333,33 |
14 000 |
0 |
0,000 |
, руб.
, руб.
Коэффициент бедности 
Индекс глубины бедности
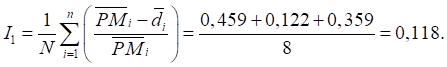
Индекс остроты бедности
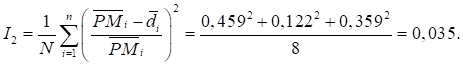
Дефицит денежного дохода обследованных домохозяйств
D=17 000 + 5 000 + 14 000 = 36 000 руб.
Оценка дефицита денежного дохода города
млн руб.
Пример 11.4.
Рассчитать абсолютное и относительное изменение покупательной способности денежных доходов населения.
|
Год |
2014 |
2015 |
|
Среднедушевой денежный доход, руб. |
27573 |
30870 |
|
Средняя цена молока жирностью 2,5%, руб./литр |
27,30 |
31,50 |
Решение
Покупательная способность денежных доходов по годам
Литров.
Литров.
Абсолютный прирост покупательной способности
DПС=ПС2015– ПС2014= 980 – 1010 = –30 литров.
Темп прироста покупательной способности
| < Предыдущая | Следующая > |
|---|
