25. Методы изучения тренда в рядах динамики

Тренд (основная тенденция) – это плавное и устойчивое систематическое изменение уровня явления во времени. Тренд отражает долгосрочную тенденцию развития явления и обусловлен наличием постоянно действующих факторов.

При изучении тренда решаются две взаимосвязанные задачи:

1. Выявление тренда и описание его качественных особенностей.

2. Количественная оценка тренда.

Методы изучения тренда:

1) Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). По укрупненным интервалам либо суммируют уровни первоначального ряда, либо исчисляют средние величины. Например, месячные данные заменяются квартальными, квартальные – годовыми и т. д. В результате случайные отклонения в уровнях первоначального ряда сглаживаются и более явно обнаруживается основная тенденция развития.

Для моментных рядов и рядов средних величин укрупнение проводится путем расчета средних уровней для новых укрупненных интервалов.

2) Метод скользящей средней Позволяет сгладить колебания, присущие ряду динамики и состоит в преобразовании исходного ряда путем замены уровней ряда на среднее значение соседних уровней. Например, если Период (интервал) сглаживания равен 3, то I-й уровень сглаженного ряда 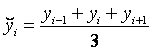. Рекомендуется применять период сглаживания с нечетным числом уровней. Недостатком сглаживания ряда является укорачивание сглаженного ряда по сравнению с фактическим, так как теряются крайние значения.

3) Аналитическое выравнивание ряда динамики позволяет по виду графического представления или на основе фактических данных подобрать аналитическую функцию, наиболее подходящую для отражения основной тенденции развития. Оценки тренда рассчитываются как функции времени

, (6.16)

Где .– теоретические уровни ряда.

При реализации этого метода выделяют следующие этапы:

1. Определение вида аналитической функции F(T) (задача Структурной идентификации).

2. Оценка параметров функции F(T) по эмпирическим данным (задача Параметрической идентификации).

3. Расчет теоретических значений тренда по найденной формуле.

Простейшими моделями, выражающими тенденцию развития, являются:

1. Линейная функция (прямая) применяется при равномерном развитии, когда абсолютные цепные приросты приблизительно одинаковы, т. е. уровни ряда изменяются в арифметической прогрессии.

2. Параболическая функция используется при равноускоренном (равнозамедленном) развитии, когда развитие идет с постоянным Ускорением (A2), т. е. абсолютные цепные приросты возрастают (уменьшаются) приблизительно равномерно.

3. Показательная функция (экспонента) . Применяют, когда темпы роста (прироста) приблизительно одинаковы, т. е. уровни ряда изменяются в геометрической прогрессии. Если A1>1, то наблюдается рост, при A1<1 – наблюдается спад. Примеры: закон Мура, согласно которому каждые полтора года производительность вычислительной техники удваиваются; сумма вклада в банке; распад радиоактивных веществ и т. д.

4. Гиперболическая функция (гипербола) 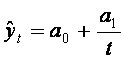. При A1>0 гиперболический тренд выражает тенденцию замедляющегося снижения уровня, стремящегося к пределу A0. При A1<0 – выражает тенденцию замедляющегося роста уровня, стремящегося к пределу A0.

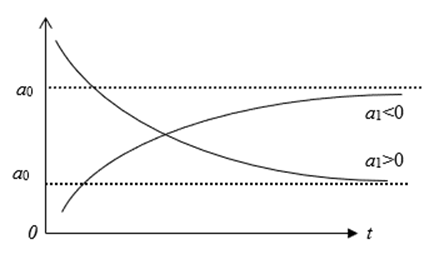
Рис.6.3. График гиперболической функции

5. Степенная функция .

6. Логарифмические функции.

Тип I . Тип II .

Тип I пригоден при описании развития с замедляющимся ростом при отсутствии предельного значения, когда с течением времени абсолютный цепной прирост DYT/t-1®0. Примеры: рост спортивных достижений, производительности труда, продуктивности скота или вообще повышения эффективности системы при ее совершенствовании без существенных преобразований.

7. Логистическая функция (S-образная кривая) 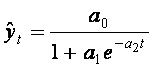позволяет описать развитие процесса в течение длительного периода времени, если он имеет тенденцию к насыщению (например, численность биологических популяций, развитие технологических инноваций, эффективность маркетинговых усилий и т. д.).

Рис.6.4. График логистической функции

Оценки параметров Ai аналитической функции F(T) можно найти с помощью Метода наименьших квадратов (МНК). Его суть заключается в том, что оценки параметров A0, A1 находят, минимизируя сумму квадратов отклонений между фактическими (эмпирическими) уровнями ряда динамики Yi и теоретическими . МНК-оценки находят, решая оптимизационную задачу

, (6.17)

Где N – число наблюдений; P – число неизвестных параметров; AI – неизвестные параметры аналитической функции F(T).

Для нахождения минимума данной функции ее частные производные приравнивают нулю и получают систему нормальных уравнений. Например, для линейной функции (прямой) система нормальных уравнений имеет вид

Тогда решение этой системы уравнений

(6.18)

Где

В дальнейшем на основе найденного уравнения тренда производится выравнивание ряда динамики, т. е. замена фактических уровней YT Уровнями , наилучшим образом аппроксимирующими исходный ряд динамики. Кроме того, с помощью уравнения тренда возможно прогнозирования ряда динамики.

< Предыдущая		Следующая >