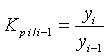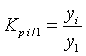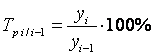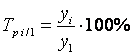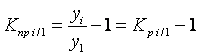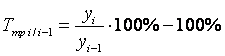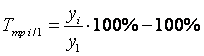23. Показатели анализа ряда динамики
Для проведения статистического анализа ряда динамики исчисляют систему показателей, сравнивая уровни ряда между собой.
В зависимости от выбора базы сравнения уровней ряда динамики различают две системы расчета показателей:
1. Базисная система, при которой каждый уровень ряда динамики УI сравнивается с уровнем, принятым за постоянную базу сравнения (за базу сравнения обычно принимают первый уровень У1).
2. Цепная система, при которой каждый уровень ряда динамики уI сравнивается с его предыдущим уровнем УI-1.
При анализе ряда динамики исчисляют следующие показатели.
1. Абсолютный прирост характеризует абсолютное изменение уровня ряда динамики.
|
Абсолютный прирост DYi/I-1=Yi–Yi-1 |
Абсолютный прирост DYi/1=Yi–Y1 |
((6.1) |
Где Yi – Уровень сравниваемого периода; Yi-1 – уровень предшествующего периода; Y1 – уровень базисного периода.
Цепные и базисные показатели связаны между собой.
Абсолютный прирост (цепной) равен разности соответствующих базисных приростов DYi/I-1=DYi/1–DYi-1/1.
Абсолютный прирост (базисный) равен сумме последовательных цепных приростов 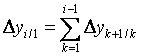 .
.
2. Темп (коэффициент) роста характеризует относительное изменение уровня ряда динамики. Показатель относительного изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста.
|
Коэффициент роста
|
Коэффициент роста
|
(6.2) |
|
Темп роста (цепной)
|
Темп роста (базисный)
|
(6.3) |
Итак, выполняется соотношение Тр=Кр×100%.
Между базисными и цепными коэффициентами роста имеется взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста ( ), а частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста (Кр I/I-1 = Кр I/1/Кр I-1/1).
), а частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста (Кр I/I-1 = Кр I/1/Кр I-1/1).
3. Темп (коэффициент) прироста во многих случаях является более наглядным показателем изменения уровня ряда динамики. Например: если сравниваемый уровень ряда больше (меньше) уровня, принятого за базу сравнения, то темп (коэффициент) прироста больше (меньше) нуля.
Темп прироста выражается в процентах, а коэффициент роста – в долях единицы.
|
Коэффициент прироста
|
Коэффициент прироста
|
(6.4) |
|
Темп прироста (цепной)
|
Темп прироста (базисный)
|
(6.5) |
Итак, выполняются соотношения: Тпр=Кпр×100%; Тпр=Тр–100%.
E Таким образом, зная один из показателей анализа ряда динамики, легко найти другие связанные с ним показатели. Например, если темп прироста составляет 5% (т. е. уровень ряда динамики увеличился), то соответственно: коэффициент прироста 0,05; темп роста 105%; коэффициент роста 1,05. Обратите внимание, если темп прироста составляет –5% (т. е. уровень ряда динамики снизился), то соответственно: коэффициент прироста –0,05; темп роста 95%; коэффициент роста 0,95.
4. Абсолютное содержание 1% прироста рассчитывают как отношение абсолютного цепного прироста к цепному темпу прироста за тот же период времени.
 (6.6)
(6.6)
| < Предыдущая | Следующая > |
|---|