12. Показатели вариации. Абсолютные и средние показатели вариации. Размах вариации
Вариация (в статистике)– это различие индивидуальных значений признака внутри изучаемой совокупности. Возникновение вариации обусловлено влиянием на изучаемое явление различных случайных и неслучайных факторов.
Хотя рассмотренные выше средние являются обобщающими характеристиками признака изучаемой совокупности, однако они не дают представления о том, какова колеблемость отдельных значений признака, насколько эти значения близки к средней. Показатели вариации позволяют оценить и исследовать колеблемость признака в совокупности.
R=Xmax – Xmin, (4.1)
Где Xmax – максимальное, Xmin – минимальное значения вариантов. Это наименее точная мера вариации, однако, она проста для вычисления.
Децильный размах
D=D9 – D1, (4.2)
Где D1 И D9 – первая (нижняя) и девятая (верхняя) децили.
Квартильный размах или интерквартильный разброс (interquartile range, IQR)
IQR=Q3 –Q1, (4.3)
Где Q1, Q3 – первый (нижний) и третий (верхний) квартили. Среди показателей размаха наиболее часто в практическом анализе используют квартильный размах.
Среднее линейное (абсолютное) отклонение
· Простое для несгруппированных данных
 , (4.4)
, (4.4)
· Взвешенное для сгруппированных данных
 . (4.5)
. (4.5)
Дисперсия
· Простая для несгруппированных данных
 , (4.6)
, (4.6)
· Взвешенная для сгруппированных данных
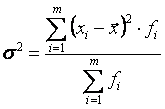 . (4.7)
. (4.7)
Можно отметить следующий недостаток этого показателя вариации – если варианты Xi имеют некоторую размерность (метр, рубль, килограмм и т. д.), то дисперсия имеет размерность в квадрате, что затрудняет ее интерпретацию (например, если средняя зарплата составляет 18 тысяч рублей, то соответствующая дисперсия может составить 500 тысяч рублей в квадрате, что лишено экономического смысла).
Этого недостатка лишено Среднее квадратическое отклонение
· Простое для несгруппированных данных
 , (4.8)
, (4.8)
· Взвешенное для сгруппированных данных
 . (4.9)
. (4.9)
Достоинством этого показателя вариации является то, что он выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
E Можно показать, что всегда справедливо неравенство L£S.
Дисперсия и среднее квадратическое отклонений являются наиболее распространенными показателями вариации.
| < Предыдущая | Следующая > |
|---|