03. Примеры решения задач 1
Пример 1.1. Произвести группировку данных о количестве детей в семье. Построить полигон распределения, кумуляту и огиву.
Исходные данные для группировки: 1, 2, 0, 1, 2, 0, 1, 1, 3, 4, 1, 4, 1, 1, 0, 1, 5, 3, 2, 1.
Решение. Так как группировочный признак является целочисленным, т. е. дискретным, то построим дискретный ряд распределения.
Ниже приведена полученная сводная таблица. На рисунке 1 приведен полигон распределения, а на рисунке 2 – кумулята и огива.
|
Количество |
Частота |
Частость |
Кумулятивный |
Кумулятивный ряд сверху |
|
0 |
3 |
0,15 (3/20) |
3 |
20 (17+3) |
|
1 |
9 |
0,45 (9/20) |
12 (3+9) |
17 (8+9) |
|
2 |
3 |
0,15 (3/20) |
15 (12+3) |
8 (5+3) |
|
3 |
2 |
0,10 (2/20) |
17 (15+2) |
5 (3+2) |
|
4 |
2 |
0,10 (2/20) |
19 (17+2) |
3 (1+2) |
|
5 |
1 |
0,05 (1/20) |
20 (19+1) |
1 |
|
Итого |
20 |
1,00 |
EНа практике в статистических таблицах приводятся только результаты вычислений. В случае необходимости промежуточные вычисления можно привести за пределами таблиц.
E Кумулятивный ряд сверху начинают строить с самого последнего интервала (с максимального значения признака).
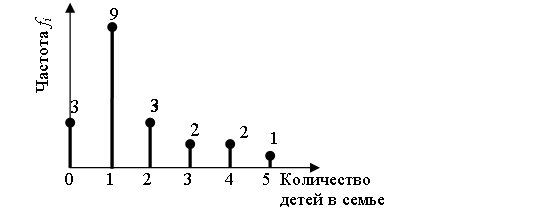
Рис. 1.1. Полигон распределения

Рис. 1.2. Графики кумуляты и огивы
Пример 1.2. Произведите группировку с равными интервалами по среднегодовой стоимости основных фондов (ОФ). В каждой группе и в целом по всем предприятиям подсчитайте: 1) количество предприятий; 2) среднегодовую стоимость основных фондов; 3) объем товарной продукции за год (ТП); 4) фондоотдачу.
Постройте гистограмму частостей, кумуляту и огиву.
|
№ п/п |
ОФ, млн руб. |
ТП, млн руб |
№ п/п |
ОФ, млн руб. |
ТП, млн руб |
|
1 |
164 |
369 |
11 |
225 |
399 |
|
2 |
147 |
134 |
12 |
189 |
354 |
|
3 |
171 |
194 |
13 |
227 |
630 |
|
4 |
267 |
377 |
14 |
216 |
453 |
|
5 |
211 |
223 |
15 |
343 |
661 |
|
6 |
123 |
91 |
16 |
296 |
1072 |
|
7 |
238 |
545 |
17 |
246 |
711 |
|
8 |
109 |
31 |
18 |
150 |
270 |
|
9 |
176 |
213 |
19 |
204 |
388 |
|
10 |
255 |
791 |
20 |
157 |
124 |
Решение. Найдем число интервалов по формуле Стерджесса (1.1) K=1+3,322×Lg 20=5,32. Положим число интервалов K=5.
Величина равного интервала (1.2)
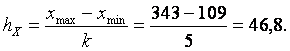
Для удобства примем H=50, XMin=100, XMax=350. Ниже в рабочей таблице приведены промежуточные результаты группировки.
Группировка предприятий по среднегодовой стоимости основных фондов
|
Номер |
Границы |
Номер |
ОФ, |
ТП, |
|
1 |
До 150 |
8 6 2 |
109 123 147 |
31 91 134 |
|
Итого |
3 |
379 |
256 | |
|
2 |
150–200 |
18 20 1 3 9 12 |
150 157 164 171 176 189 |
270 124 369 194 213 354 |
|
Итого |
6 |
1007 |
1524 | |
|
3 |
200–250 |
19 5 14 11 13 7 17 |
204 211 216 225 227 238 246 |
388 223 453 399 630 545 711 |
|
Итого |
7 |
1567 |
3349 | |
|
4 |
250–300 |
10 4 16 |
255 267 296 |
791 377 1072 |
|
Итого |
3 |
818 |
2240 | |
|
5 |
300 и выше |
15 |
343 |
661 |
|
Итого |
1 |
343 |
661 | |
|
Всего |
20 |
4114 |
8030 |
EОбратите внимание, что единица совокупности №18 (значение признака 50) попала во вторую группу. Условимся, что в случае, если значение признака совпадает с границей группы, то такой элемент относят к следующей группе.
В сводной таблице приведены итоговые результаты группировки.
Сводная таблица
|
Номер группы |
Границы |
Частота |
Частость |
ОФ, млн руб. |
ТП, млн руб. |
Фондо-отдача |
Кумулятивный ряд | |
|
Снизу |
Сверху | |||||||
|
1 |
До 150 |
3 |
0,15 |
379 |
256 |
0,675 |
3 |
20 |
|
2 |
150-–200 |
6 |
0,30 |
1007 |
1524 |
1,513 |
9 |
17 |
|
3 |
200—250 |
7 |
0,45 |
1567 |
3349 |
2,137 |
16 |
11 |
|
4 |
250–300 |
3 |
0,15 |
818 |
2240 |
2,738 |
19 |
4 |
|
5 |
300 и выше |
1 |
0,05 |
343 |
661 |
1,927 |
20 |
1 |
|
Всего |
20 |
1,00 |
4114 |
8030 |
1,952 |
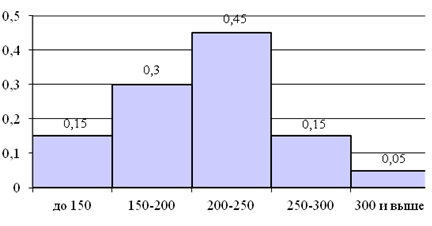
Рис. 1.3. Гистограмма частостей

Рис. 1.4. Графики кумуляты и огивы
Анализируя сводную таблицу можно сделать вывод, что с ростом размеров предприятия фондоотдача возрастает. Однако это не выполняется для самого крупного предприятия (№15), что свидетельствует о недостаточно эффективном использовании основных фондов.
Пример 1.3. На основе данных примера 2 провести сложную группировку, подсчитав число предприятий попавших в каждую группу.
Решение. Величина равного интервала при группировке по объему товарной продукции
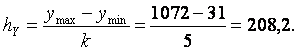
Для удобства примем HY=200, YMin=0, YMax=1000. В таблице приведены результаты группировки.
Группировка предприятий
по стоимости основных фондов и товарной продукции
|
ТП ОФ |
До 200 |
200–400 |
400–600 |
600–800 |
800 и выше |
Всего |
|
До 50 |
3 |
– |
– |
– |
– |
3 |
|
50-–100 |
2 |
4 |
– |
– |
– |
6 |
|
100—150 |
– |
3 |
2 |
2 |
– |
7 |
|
150–200 |
– |
1 |
– |
1 |
1 |
3 |
|
200 и выше |
– |
– |
– |
1 |
– |
1 |
|
Всего |
5 |
8 |
2 |
4 |
1 |
20 |
Анализируя эту таблицу можно сделать вывод, что предприятия, «попавшие» в нижний левый угол таблицы, неэффективно используют свои основные фонды, тогда как предприятия, «попавшие» d верхний правый угол, используют их более эффективно.
Пример 1.4. На основе данных примера 2 составить ряд распределения с неравными равнонаполненными интервалами. Группировочный признак – среднегодовая стоимость основных фондов. Построитm гистограмму частостей.
Решение. Разобьем совокупность на группы равного объема с числом единиц F=N/K=20/5=4. Результаты выделения групп приведены в таблице.
Группировка предприятий по среднегодовой стоимости основных фондов (равнонаполненные интервалы)
|
Номер |
Границы |
Номер |
ОФ, |
ТП, |
|
1 |
До 150 |
8 6 2 18 |
109 123 147 150 |
31 91 134 270 |
|
Итого |
4 |
429 |
526 | |
|
2 |
150–180 |
20 1 3 9 |
157 164 171 176 |
124 369 194 213 |
|
Итого |
4 |
668 |
900 | |
|
3 |
180–220 |
12 19 5 14 |
189 204 211 216 |
354 388 223 453 |
|
Итого |
4 |
820 |
1418 | |
|
4 |
220–250 |
11 13 7 17 |
225 227 238 246 |
399 630 545 711 |
|
Итого |
4 |
936 |
2285 | |
|
5 |
250 и выше |
10 4 16 15 |
255 267 296 343 |
791 377 1072 661 |
|
Итого |
4 |
1161 |
2901 | |
|
Всего |
20 |
4114 |
8030 |
Рассчитаем относительные плотности ![]() (1/3) с учетом того, что величины интервалов H1=50, H2=30, H3=40, H4=30, H5=100.
(1/3) с учетом того, что величины интервалов H1=50, H2=30, H3=40, H4=30, H5=100.
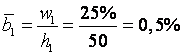 ;
;  ;
;  ;
;
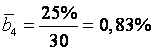 ;
; 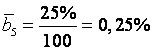 .
.
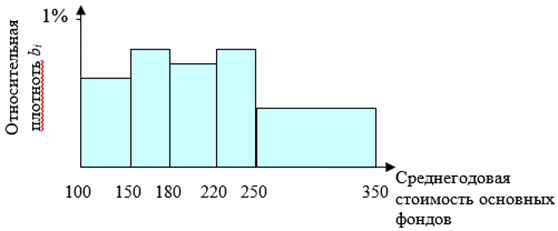
Рис. 1.5. Гистограмма частостей
| < Предыдущая | Следующая > |
|---|