Заключение
Заключение
Вот такими оказались “начала” этой могучей науки. Ее течение из глубины столетий к нашим дням и в будущее все более активно охватывает различные разделы математики, других наук, рождает новые научные теории. К примеру, одна из них – нестандартный анализ – позволила сделать глубокие обобщения идей Ньютона, Лейбница, предвосхищая, возможно, достижения математики на многие годы вперед. Стремительно развивается дискретная математика, изучающая дискретные множества. Частью этого направления является, например, математическая логика. Идеи математического анализа органично вплелись в построение многих технических наук, активно их развивая, а указанные науки, в свою очередь, “поставляют” для самого математического анализа новые проблемы, способствующие его совершенствованию.
Математика, в отличие от других наук, создает образы, которые находятся вне потока времени. Мир математики существует в настоящем, делающем бессмысленными понятия прошлого и будущего. С точки зрения этой науки, время – величина, ничем не отличающаяся от других величин. Обладая способностью описывать объекты реального мира и объекты воображаемые, конструируемые средствами математического моделирования, мы не говорим о событиях желаемых, важных или второстепенных. Вместе с тем, математическое моделирование, являясь формой межпредметной деятельности, побуждает нас искать причинно–временные отношения, проникать тем самым в суть естественных наук.
Каждая научная теория ценна возможностью предсказать будущие события. Возможность предсказания основана на том, что закономерности, наблюдавшиеся в прошлом, повторяются в будущем. Возможность предсказания кроется в гипотетическом продолжении прошлого в будущем. Математика способна сделать успешным такое прогнозирование, вовлекая в него свои умозрительные построения.
К примеру, французский астроном Леверье в 1846 г. “на кончике пера” обнаружил новую планету Нептун, вычисляя возмущения орбиты уже известной в то время планеты Уран. Английский физик Максвелл, анализируя телеграфное уравнение, предсказал существование электромагнитных волн, которые экспериментально уже позже обнаружил немецкий физик Герц. Выдающийся русский механик Н. Е. Жуковский математически предсказал возможность фигур высшего пилотажа – и вскоре “мертвая петля” была впервые выполнена армейским офицером П. Н. Нестеровым.
Мудрость математики, бесстрастно проникающей во все науки, всегда актуальна для свободного развития естествознания и техники, исключающего конъюнктурную целесообразность действий при достижении цели.
Процесс математического моделирования чаще всего не может быть обозначен жесткой последовательностью операций. Для нас важны прежде всего его принципы. Математическое моделирование в наше время достигает той степени совершенства, когда вместо простого перебора вариантов путей решения задачи действует интуиция поиска оптимальных путей получения результата, подкрепленная мощными возможностями ЭВМ. Вот почему особую роль в мышлении для специалиста по математическому моделированию играет творческая фантазия, которая заставляет пытливый ум видеть разнообразие окружающего мира. Элементы математического моделирования, обозначаемые в данной книге, следует рассматривать лишь как частицы первоначального опыта использования богатства математических знаний.
Шахматы и математика часто дополняют друг друга. Вероятно, поэтому представляется возможным определить перспективы развития математического анализа шахматным языком:
ВСЕ ДЕБЮТЫ УЖЕ ИЗВЕСТНЫ,
НОВОЕ – В ИХ РАЗВИТИИ.
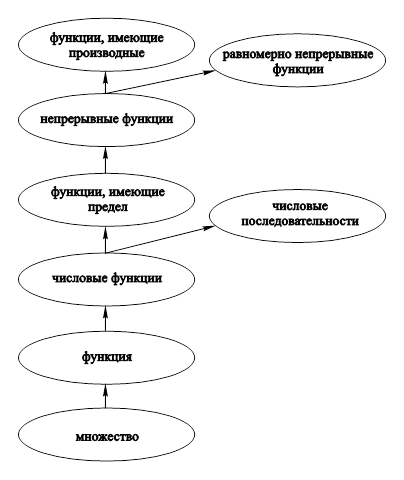
ВАЖНЕЙШИЕ ПОНЯТИЯ, ИСПОЛЬЗУЕМЫЕ В МАТЕМАТИЧЕСКОМ АНАЛИЗЕ
ИМЕННОЙ УКАЗАТЕЛЬ
1. Аристотель (384 – 322 до н. э.)
2. Архимед (287 – 212 до н. э.)
3. Больцано Б. (1781 – 1848)
4. Бурбаки Н.
5. Вейерштрасс К. (1815 – 1897)
6. Галуа Э. (1811 – 1832)
7. Гаусс К. (1777 – 1855)
8. Ганкель (1839 – 1873)
9. Гильберт Д. (1862 – 1943)
10. Даламбер Ж. (1717 – 1783)
11. Дедекинд Р. (1831 – 1916)
12. Декарт Р. (1596 – 1650)
13. Кантор Г. (1845 – 1918)
14. Колмогоров А. Н. (1903 – 1987)
15. Кронекер Л. (1823 – 1891)
16. Лейбниц Г. (1646 – 1716)
17. Линдеман Ф. (1852 – 1939)
18. Лобачевский Н. И. (1792 – 1856)
19. Лузин Н. Н. (1883 – 1950)
20. Ньютон И. (1643 – 1727)
21. Омар Хайям (1048 – 1123)
22. Пифагор (VI в. до н. э.)
23. Понтрягин Л. С. (1908 – 1988)
24. Пеано Дж. (1858 – 1932)
25. Риман Бернхард (1826 – 1866)
26. Рассел Б. (1872 – 1970)
27. Ферма П. (1601 – 1665)
28. Федоров Е. С. (1853 – 1919)
29. Эйлер Л. (1707 – 1783)
| < Предыдущая |
|---|