4.4. Оценка с помощью интервалов
Оценка параметров с помощью интервалов заключается в нахождении интервалов, называемых Доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров. Интервальная оценка определяется двумя числами - концами интервала.
Пусть найденная по данным выборки величина Q* служит оценкой неизвестного параметра Q. Оценка Q* определяется тем точнее, чем меньше
|Q - Q*|, т. е. чем меньше d в неравенстве |Q - Q*|< d, d > 0.
Доверительной вероятностью (Надежностью) оценки Q* параметра Q называется вероятность ¡, с которой оценивается неравенство |Q - Q*|< D.
Число A=1 - ¡ называется Уровнем значимости, определяющим вероятность того, что оцениваемый параметр не попадет в доверительный интервал.
Обычно задается надежность ¡ и определяется D. Чаще всего вероятность ¡ задается значениями от 0.95 и выше. Неравенство |Q - Q*|< D Можно записать в виде
- D < Q - Q* < D или Q* - D < Q < Q* + D.
Доверительным интервалом называется интервал (Q* - D, Q* + D), который покрывает неизвестный параметр Q с заданной надежностью.
Определение доверительного интервала для среднего значения нормально распределенной измеряемой случайной величины Х При известной дисперсии ![]() .
.
Нам уже известно, что 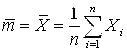 . Можно показать [1-5], что
. Можно показать [1-5], что  (сумма
(сумма ![]() нормально распределенных случайных величин
нормально распределенных случайных величин ![]() сама является нормальной).
сама является нормальной).
Зададим доверительную вероятность ¡ и найдем доверительный интервал (![]() - D,
- D, ![]() + D), который покрывал бы неизвестный параметр
+ D), который покрывал бы неизвестный параметр ![]() с заданной надежностью ¡.
с заданной надежностью ¡.
Согласно формуле В (Свойства нормального распределения, раздел 3)
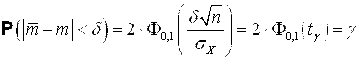 . (4.1)
. (4.1)
Таким образом, для отыскания величины Доверительной границы случайного отклонения результатов наблюдений по Доверительной вероятности ¡ имеем уравнение:
![]() , где
, где 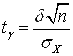 ,
,
Где значение ![]() находим по таблице Лапласа (приложение 1),
находим по таблице Лапласа (приложение 1), ![]() .
.
Пример 4.7. По результатам наблюдений была найдена оценка неизвестного математического ожидания M случайной величины ![]() если точечная оценка
если точечная оценка ![]() =10.2, а дисперсия оценки
=10.2, а дисперсия оценки ![]() =4. Требуется оценить доверительный интервал для оценки математического ожидания по 36-ти наблюдениям с заданной надежностью ¡=0.99.
=4. Требуется оценить доверительный интервал для оценки математического ожидания по 36-ти наблюдениям с заданной надежностью ¡=0.99.
Решение. Из (4.1) следует, что ![]() . Отсюда получаем, что
. Отсюда получаем, что 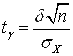 =2.58 и половина искомого интервала
=2.58 и половина искомого интервала 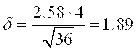 . Так как
. Так как ![]() , то с вероятностью 0.99 доверительный интервал для оценки математического ожидания:
, то с вероятностью 0.99 доверительный интервал для оценки математического ожидания: ![]() .
.
Со случаем, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна, можно ознакомится в [3, 4, 6].
| < Предыдущая | Следующая > |
|---|