4.2. Вариационный ряд. Полигон частот и гистограмма эмпирическая функция распределения

Пусть Х — некоторый признак изучаемого объекта или явления (срок службы электролампы, вес студента, диаметр шарика для подшипника и т. п.). Генеральной совокупностью является множество всех возможных значений этого признака, а результаты N наблюдений над признаком Х дадут нам выборку объема N — первоначальные статистические данные, значения (простая выборка, не сгруппированные данные)

При этом значение получено при первом наблюдении случайной величины Х, – при втором наблюдении той же случайной величины и т. д.

Выборку преобразуют в Вариационный ряд, располагая результаты наблюдений в порядке возрастания: Каждый член Вариационного ряда называется Вариантой.

Пример 4.1.

1. Измерена масса тела 10-ти детей 6-ти лет. Полученные данные образуют простой статистический ряд: 24 22 23 28 24 23 25 27 25 25.

2. Из 10000 выпущенных на конвейере электрических лампочек отобрано 300 штук для проверки качества всей партии. Здесь а

Отдельные значения статистического ряда называются Вариантами. Если варианта ХI появилась M раз, то число M называют Частотой, а ее отношение к объему выборки M/N – Относительной частотой.

Последовательность вариант, записанная в возрастающем (убывающем) порядке, называется Ранжированным рядом.

Пример 4.2. Для ранжированного ряда: 23 23 24 24 25 25 25 27 28 в нижеприведенной таблице в первой строке записаны все значения величины (варианты), во второй – соответствующие им частоты (безынтервальный вариационный ряд), в третьей – накопленные частоты, в четвертой – относительные частоты (табл.4.1).

Таблица 4.1. Значения вариант и их частот

Х	22	23	24	25	27	28
Ni	1	2	2	3	1	1
NН	1	3	5	8	9	10
	0.1	0.2	0.2	0.3	0.1	0.1

Полигоном частот называют ломаную линию, отрезки которой соединяют точки с координатами (ХI; Ni) (рис. 4.1).

Отметим, что сумма частот статистического ряда равна объему выборки. Часто статистический ряд составляют, используя относительные частоты вариант: (M — количество различных вариант). Сумма относительных частот равна единице.

Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки с координатами (ХI; Hi).

А)	Б)

Рисунок 4.1. Полигон частот а), кумулятивная кривая б)

Эмпирическим аналогом графика интегральной функции распределения является Кумулятивная кривая (Кумулята). Для ее построения на оси ОХ откладывают значения вариант, на оси ОY – накопленные частоты или относительные частоты. Полученная плавная кривая называется кумулятой.

В том случае, если выборка представлена большим количеством различных значений непрерывной случайной величины, то группировку данных проводят в виде интервального вариационного ряда (ИВР). Для этого диапазон варьирования признака разбивают на несколько (5–10) равных интервалов и указывают количество вариант, попавших в каждый интервал.

Алгоритм построения интервального вариационного ряда.

1. Исходя из объема выборки (N), определить количество интервалов (K) (см. табл. 4.2).

Таблица 4.2.Рекомендуемое соотношение Объем выборки-число интервалов

N	25–40	40–60	60–100	100–200	>200
K	5–6	6–8	7–10	8–12	10–15

2. Вычислить размах ряда: R=Xmax – Xmin

3. Определить ширину интервала: H=R/(K–1)

4. Найти начало первого интервала X0 = Xmin – H/2

5. Составить интервальный вариационный ряд.

Графическим изображением ИВР является Гистограмма. Для ее построения на оси ОХ откладывают интервалы шириной H, на каждом интервале строят прямоугольник высотой M/H. Величина M/H называется Плотностью частоты. Гистограмма является эмпирическим аналогом графика дифференциальной функции распределения.

Пример 4.3. Измерена масса тела 100 женщин 30 лет, получены значения от 60 до 90 кг. Построить интервальный вариационный ряд (табл. 4.3) и гистограмму.

Таблица 4.3. Интервальный вариационный ряд

Интервал	Середина интервала	M	M/H
60–65	62.5	14	2.8
65–70	67.5	32	6.4
70–75	72.5	28	5.6
75–80	77.5	14	2.8
80–85	82.5	7	1.4
85–90	87.5	2	0.4

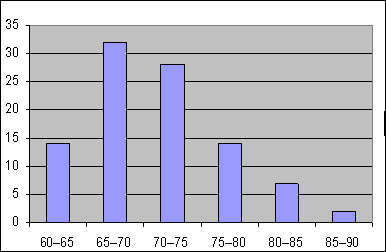
Рисунок 4.2. Гистограмма

Эмпирическая функция распределения находится по следующей формуле (отношение накопленных частот к объему выборки):

(4.1)

< Предыдущая		Следующая >