6.3. Оптимальный портфель ценных бумаг

Задача о формировании оптимального портфеля ценных бумаг – это задача о распределении капитала, который участник рынка хочет потратить на покупку набора ценных бумаг, по различным видам ценных бумаг, удовлетворяющих возможность получения некоторого дохода.

Из характеристик ценных бумаг наиболее значимы две: эффективность и рискованность. Т. к. эффективность – это некоторый обобщенный показатель дохода или прибыли, то ее считают случайной величиной, а ее математическое ожидание обозначают как . Рискованность ценных бумаг отождествляют со средним квадратическим отклонением, при этом дисперсию обычно называют вариацией и обозначают как , т. е.:

, где .

Примем следующие обозначения:

– номер вида ценных бумаг; –доля капитала, потраченная на закупку ценных бумаг -го вида (сумма всех долей равна единице); – эффективность ценных бумаг -го вида, стоящих одну денежную единицу; –математическое ожидание эффективности ; –ковариация ценных бумаг -го и -го видов; – вариация (дисперсия) эффективности ;– рискованность ценных бумаг -го вида; – эффективность портфеля (набора) ценных бумаг.

Тогда, математическое ожидание эффективности портфеля ценных бумаг:

,

Вариация портфеля ценных бумаг:

,

Риск портфеля ценных бумаг:

.

Следовательно, математическая формализация задачи формирования опти­мального портфеля ценных бумаг следующая.

Найти такое распределение долей капитала, которое минимизирует вариацию эффективности портфеля, при заданной ожидаемой эффективности портфеля .

Тогда, если оптимальное решение обозначить как *, то:

() – означает рекомендацию вложить долю капитала в ценные бумаги ‑го вида; () – означает возможность проведения операции “short sale”, т. е. краткосрочного вложения доли капитала в более доходные ценные бумаги.

Если на рынке есть безрисковые ценные бумаги, то решение задачи о формировании портфеля ценных бумаг приобретает новое качество.

Пусть:

– эффективность безрисковых ценных бумаг; – доля капитала, вложенного в безрисковые ценные бумаги; – средняя ожидаемая эффективность рисковой части портфеля; – вариация рисковой части портфеля; – среднее квадратическое отклонение эффективности рисковой части портфеля.

Тогда в рисковую часть портфеля вложена часть всего капитала, а т. к. считается, что безрисковые ценные бумаги некоррелированы с остальными, то ожидаемая эффективность всего портфеля ценных бумаг:

,

Вариация портфеля ценных бумаг:

,

Риск портфеля ценных бумаг:

.

Допустим, что задача состоит в нахождении распределения капитала, при формировании оптимального портфеля ценных бумаг заданной эффективности, состоящего из трех видов ценных бумаг: безрисковых эффективности 3 и некоррелированных рисковых, с ожидаемой эффективностью 5 и 9, риски которых равны 4 и 6, т. е.:

, , , , .

Тогда, вариации некоррелированных рисковых ценных бумаг первого и второго вида:

,

.

Следовательно, матрица ковариаций рисковых видов ценных бумаг и вектор‑столбец Ожидаемой эффективности рисковых видов ценных бумаг имеют вид:

,

.

Пусть – двухмерный вектор-столбец, компоненты которого равны 1, т. е.:

.

Тогда значение вектора-столбца оптимальных значений долей, вложенных в рисковую часть портфеля ценных бумаг:

,

Где:

,

,

,

,

.

Т. е.:

.

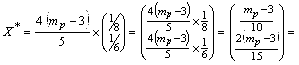
Таким образом, доли рисковых ценных бумаг в оптимальном портфеле:

, .

Следовательно, доля безрисковых ценных бумаг в оптимальном портфеле:

.

Т. к. необходимость проведения операции “short sale” возникает, когда , то в данном случае, необходимость проведения операции “short sale” возникает, когда :

, т. е. когда .

< Предыдущая		Следующая >