5.3. Задача о «Расшивке узких мест производства»
Задача о «расшивке узких мест производства» заключается в том, что, например, когда в процессе производства происходит изменение объема какого-либо ресурса, используемого в производстве, то, соответственно изменяется план производства и прибыль предприятия, получаемая от реализации готовой продукции. Это может происходить по различным причинам, например: сломался станок, поставщик предлагает сырье в большем количестве и т. п.
Поэтому, когда какой-либо ресурс используется полностью, то уменьшение объема этого ресурса, может повлиять на всю структуру плана производства и прибыль предприятия. Следовательно, такой ресурс, образующий «узкие места производства», желательно иметь с некоторым запасом, т. е. заказывать дополнительно, чтобы сохранить структуру плана производства и получить возможность увеличить прибыль предприятия.
Для примера возьмем данные и результаты вычислений из п.5.1. и п. 5.2., где определено, что первый и второй ресурс используются полностью, и, соответственно, именно их нужно заказывать дополнительно. Но в таких объемах, чтобы сохранить структуру ранее найденной программы производства, и с условием, что от поставщика можно получить дополнительно не более одной трети первоначально выделенного объема ресурса любого вида. Следовательно, задача сводится к нахождению объемов приобретения дополнительных ресурсов, удовлетворяющих указанным условиям, и вычислению дополнительной возможной прибыли.
Тогда, пусть ![]() – вектор дополнительных объемов ресурсов:
– вектор дополнительных объемов ресурсов:
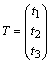 ,
,
При этом для сохранения структуры производственной программы, должно выполняться условие устойчивости двойственных оценок:
![]() .
.
Т. к. ![]() , то задача состоит в том, чтобы найти вектор:
, то задача состоит в том, чтобы найти вектор:
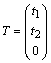 ,
,
Максимизирующий суммарный прирост прибыли:
![]() , (23)
, (23)
При условии сохранения структуры производственной программы:
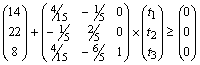 , (24)
, (24)
Предполагая, что можно надеяться получить дополнительно не более одной трети первоначального объема ресурса каждого вида, т. е.:
 , (25)
, (25)
Причем дополнительные объемы ресурсов, по смыслу задачи, не могут быть отрицательными, т. е.:
![]() ,
, ![]() . (26)
. (26)
Т. к. неравенства (24) и (25) должны выполняться одновременно, то их можно переписать в виде одной системы неравенств:
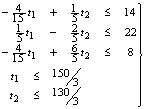 . (27)
. (27)
Таким образом, получена задача линейного программирования: максимизировать функцию (23) при условиях (26) и (27).
Эту задачу с двумя переменными можно решить графически:

Номерами на графике обозначены линии, соответствующие номерам ограничений в системе ограничений (27).
На графике видно, что система линейных неравенств (26), (27), образует область допустимых решений, ограниченную прямыми:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
При этом линии уровня функции (23) перпендикулярны вектору-градиенту ![]() и образуют семейство параллельных прямых (градиент указывает направление возрастания функции). Наибольшего значения функция (23) достигает в точке
и образуют семейство параллельных прямых (градиент указывает направление возрастания функции). Наибольшего значения функция (23) достигает в точке ![]() Пересечения прямых:
Пересечения прямых:
![]() и
и ![]() .
.
Координаты этой точки и определяют искомые объемы дополнительных ресурсов. Следовательно, программа «расшивки узких мест производства имеет вид:
![]() ,
, ![]() ,
, ![]() .
.
И прирост прибыли составит:
![]() .
.
Сводка результатов по пунктам 1-3 приведена в таблице 5.
|
Таблица 5 – Сводка результатов |
| |||||||
|
|
30 |
11 |
45 |
6 |
B |
|
|
|
|
|
3 |
2 |
6 |
0 |
150 |
0 |
6 |
50 |
|
4 |
2 |
3 |
5 |
130 |
0 |
3 |
| |
|
4 |
3 |
2 |
4 |
124 |
8 |
0 |
0 | |
|
|
22 |
0 |
14 |
0 |
1290 |
| ||
|
|
0 |
7 |
0 |
9 | ||||
| < Предыдущая | Следующая > |
|---|