07. Задача о кратчайшем пути
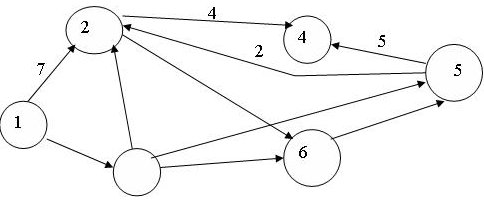
Как кратчайшим путем попасть из одной вершины графа в другую? В терминах производственного менеджмента: как кратчайшим путем (и, следовательно, с наименьшим расходом топлива и времени, наиболее дешево) попасть из пункта А в пункт Б? Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной. Рассмотрим пример (Рис. 8.7).
Рис. 8.7. Исходные данные к задаче о кратчайшем пути
Ситуацию можно описать не только ориентированным графом с весами, приписанными дугам, но и таблицей (Табл. 8.4). В этой таблице двум вершинам - началу пути и концу пути - ставится в соответствие время в пути. В Табл. 8.4 рассматриваются пути без промежуточных остановок. Более сложные маршруты составляются из элементарных отрезков, перечисленных в Табл. 8.4.
Таблица 8.4
Исходные данные к задаче о кратчайшем пути
|
Конец дуги |
Время в пути |
|
|
1 |
2 |
7 |
|
1 |
3 |
1 |
|
2 |
4 |
4 |
|
2 |
6 |
1 |
|
3 |
2 |
5 |
|
3 |
5 |
2 |
|
3 |
6 |
3 |
|
5 |
2 |
2 |
|
5 |
4 |
5 |
|
6 |
5 |
3 |
Спрашивается в задаче: как кратчайшим путем попасть из вершины 1 в вершину 4?
Решение. Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается.
Для исходных данных, представленных на Pис. 8.7 и в Табл. 8.4, в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому C(3)=1. Кроме того, очевидно, что C(1)=0.
В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение: C(4)=Min{C(2)+4;C(5)+5}.
Таким образом, проведена реструктуризация (упрощение) задачи – нахождение C(4) сведено к нахождению C(2) и C(5).
В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение: C(5)=Min{C(3)+2;C(6)+3}.
Мы знаем, что C(3)=1. Поэтому: C(5)=Min{3;C(6)+3}.
Поскольку очевидно, что C(6)- положительное число, то из последнего соотношения вытекает, что C(5)=3.
В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение: C(2)=Min{C(1)+7;C(3)+5;C(5)+2}.
Нам известно, что C(1)=0, C(3)=1, C(5)=3. Поэтому: C(2)=Min{0)+7;1)+5;3+2}=5.
Теперь мы можем найти C(4): C(4)=Min{C(2)+4;C(5)+5} = Min{5+4;3+5}=8.
Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков: 1 ð 3 ð 5 ð 4.
Задача о кратчайшем пути для конкретных исходных данных (Рис. 8.7 и Табл. 8.4) полностью решена.
Оптимизационные задачи на графах, возникающие при подготовке управленческих решений в производственном менеджменте, весьма многообразны. Рассмотрим в качестве примера еще одну задачу, связанную с перевозками.
| < Предыдущая | Следующая > |
|---|