11. Вычисление площади поверхности вращения, объёма тела вращения, объёма по известным поперечным сечениям

1. Площадь поверхности, образующейся при вращении кривой ( - непрерывно – дифференцируемая функция), вычисляется по формуле:

.

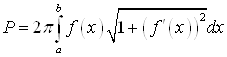2. Если вращающая кривая задана параметрически , то

.

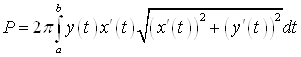3. Объём тела, полученного при вращении фигуры, ограниченной линиями и вокруг оси равен

,

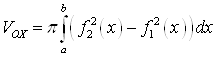И вокруг оси

.

4. С помощью определенного интеграла можно вычислить объём тела, если известна площадь поперечного сечения плоскостью, параллельной какой – либо из координатных плоскостей (например ) - :

.

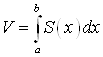Примеры:

А) вычислить поверхность сферы с центром в начале координат.

Б) вычислить объём тела ограниченного поверхностью эллипсоида .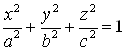

В) вычислить площадь поверхности, образованной вращением астроиды .

Решение:

А) поверхность сферы получается вращением верхней половины окружности вокруг оси .

В соответствие с формулой (п. 1)

.

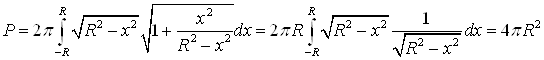Б) при пересечении эллипсоида и плоскости получается эллипс с полуосями и .

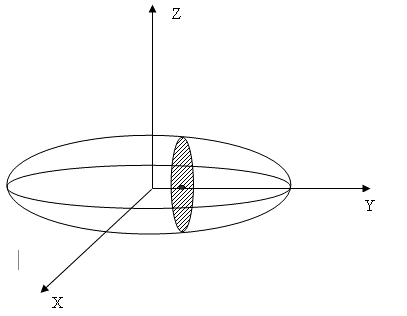
Площадь такого эллипса . Таким образом,

.

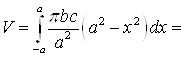
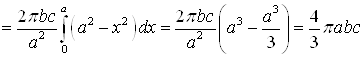В) поскольку астроида симметрична относительно оси , то можно вычислить половину искомой площади 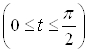и результат удвоить.

.

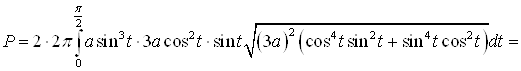
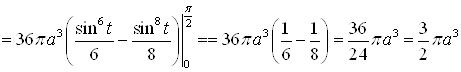< Предыдущая		Следующая >