09. Вычисление длины дуги с помощью определённого интеграла

1. Пусть дуга разбита на частей точками , ,…,, точки , соединены отрезками прямой. Пусть длина соответствующего отрезка полученной ломаной. Тогда длина всей ломаной

.

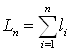Если по всем возможным разбиениям, то кривая называется спрямляемой, а - длиной дуги.

2. Пусть дуга задана параметрически , , . Если функции и - непрерывно дифференцируемы, то дуга спрямляема, а длина дуги может быть вычислена по формуле

.

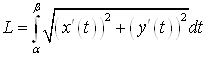3. Если кривая задана в декартовых координатах и - непрерывна, то

.

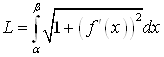4. В полярной системе координат кривая задаётся уравнением . Если - непрерывно дифференцируема, то

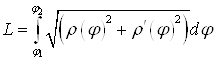
Примеры: вычислить

А) длину одной арки циклоида .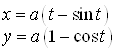

Б) длину логарифмической кривой и до .

В) длину кардиоиды .

Решение:

А) дуга задана параметрически, в соответствие с формулой п. 2.

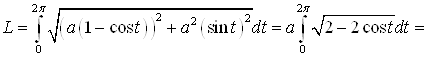
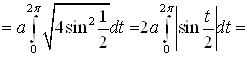
=|поскольку, а , то , и знак модуля можно снять|=

.

Б) в данном случае кривая задана декартовыми координатами (п. 3)

.

В) кардиоида задана в полярных координатах . Кривая замкнута: .

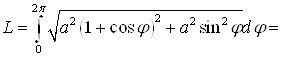|поскольку кривая симметрична

Относительно полярной оси|

|на рассматриваемом отрезке |.

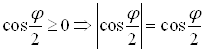< Предыдущая		Следующая >