07. Вычисление площади плоской фигуры с помощью определенного интеграла

1. Площадь криволинейной трапеции (фигуры, ограниченной кривой , прямыми , и отрезком оси ) вычисляется по формуле:

.

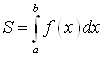2. Площадь криволинейного сектора, ограниченного лучами , и кривой в полярной системе координат,

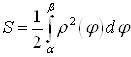
3. Площадь криволинейной трапеции ограниченной прямыми , , отрезком оси и кривой, заданной параметрически вычисляется по формуле:

.

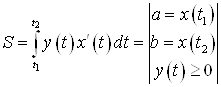Примеры: найти площадь, ограниченную

А) кривыми , ,

Б) лемнискатой Бернулли ,

В) эллипсом .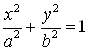

Решение:

А) Линии и пересекаются в двух точках: (-1,0) и (0,1). Область, площадь которой следует вычислить, ограничена сверху кривой и снизу .

.

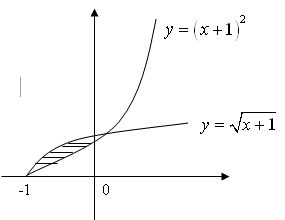
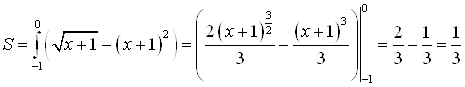Б) Функция определена при , т. е. на двух промежутках и . Область, ограниченная лемнискатой Бернулли состоит из 4х одинаковых частей: , - площадь криволинейного сектора, ограниченного лучами , и кривой .

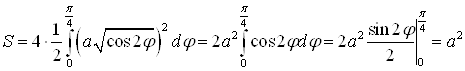
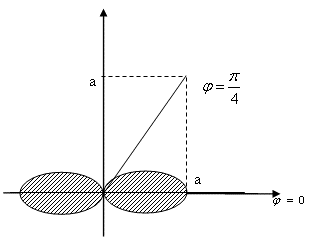
Таким образом, площадь, ограниченная лемнискатой Бернулли, равна площади квадрата со стороны .

В) Уравнение эллипса удобно задать в параметрическом виде:

,

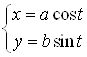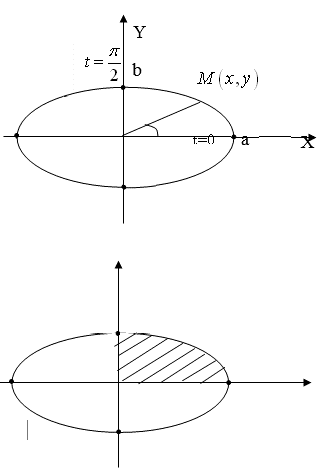
Площадь, ограниченная эллипсом , соответствует параметру , соответствует .

Таким образом:

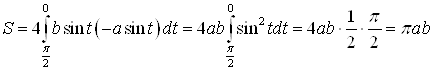
< Предыдущая		Следующая >