05. Метод интегрирования по частям и замена переменной в определенном интеграле

1. Если функции и на промежутке имеют непрерывные производные, то

.

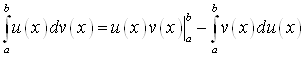Примеры:

А) Вычислить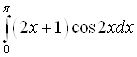

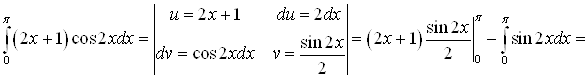
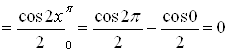Решение:

.

Б) Получить рекуррентное соотношение для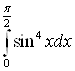

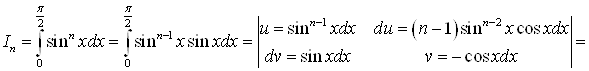
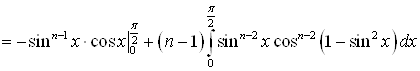
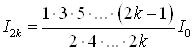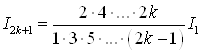Решение:

,

,

2. Пусть интегрируема на , функция строго монотонна на промежутке причем ; и имеют непрерывную производную.

Тогда .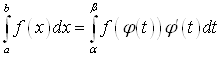

Примеры: вычислить интегралы:

А) 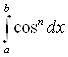, Б) ,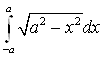

В) 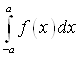, если - нечетная на функция и если - четная функция на ,

Г) .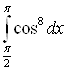

Решение:

А) .

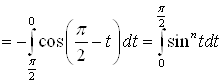Б)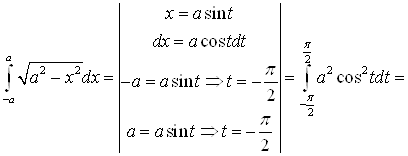

.

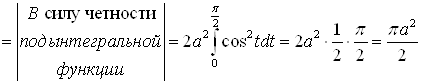В)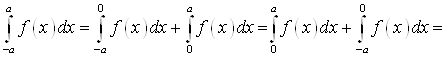

.

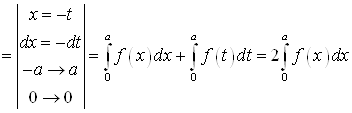Г) .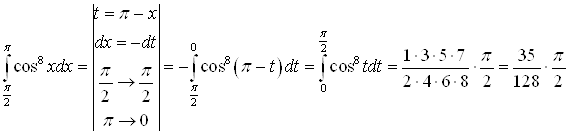

< Предыдущая		Следующая >