03. Свойства интеграла Римана
1. ![]() .
.
2. ![]() .
.
3. Определенный интеграл обладает свойством линейности:
Если ![]() и
и ![]() интегрируемы на
интегрируемы на ![]() , то
, то
А) ![]() функция
функция ![]() - интегрируема на
- интегрируема на ![]() и
и ![]()
Б) ![]() - интегрируема на
- интегрируема на ![]() и
и ![]() .
.
4. Определённый интеграл обладает свойством адитивности:
Если ![]() интегрируема на
интегрируема на ![]() и
и ![]() , то она интегрируема на
, то она интегрируема на ![]() и
и 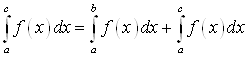 .
.
5. Если ![]() интегрируема на
интегрируема на ![]() , то
, то ![]() тоже интегрируема на
тоже интегрируема на ![]() и справедливо неравенство
и справедливо неравенство
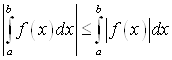 .
.
6. Если ![]() и
и ![]() интегрируемы на
интегрируемы на ![]() и выполнено неравенство
и выполнено неравенство
![]()
![]() , то
, то  .
.
7. Если ![]() ,
, ![]() , то
, то
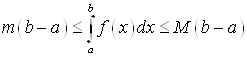 .
.
8. Теорема (О среднем значении)
Пусть ![]() - непрерывна на
- непрерывна на ![]() , тогда
, тогда 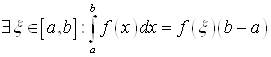 .
.
Число 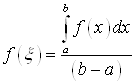 называется средним значением функции на промежутке
называется средним значением функции на промежутке ![]() .
.
9. Если функция ![]() непрерывна на
непрерывна на ![]() , то
, то  - дифференцируема и
- дифференцируема и ![]() .
.
Следствие: любая непрерывная функция на ![]() имеет первообразную.
имеет первообразную.
10. Формула Ньютона – Лейбница.
Если ![]() - какая-либо первообразная
- какая-либо первообразная ![]() , то
, то
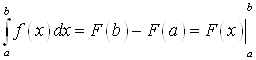 .
.
Пример 1: Вычислить определённые интегралы
А) 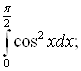 Б)
Б) 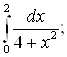 В)
В)  .
.
А) 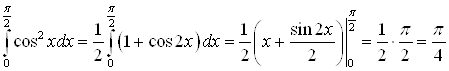 .
.
Б)  .
.
В) 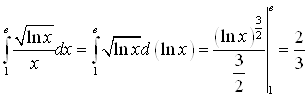
Пример 2. Вычислить пределы, используя понятия определенного интеграла
А) 
Б) 
А) Выражение под знаком предела представляет собой интегральную сумму для функции ![]() на промежутке
на промежутке ![]() для разбиения, делящего отрезок на
для разбиения, делящего отрезок на ![]() равных частей
равных частей ![]() и выбора точек
и выбора точек ![]() . Поскольку функция
. Поскольку функция ![]() На промежутке
На промежутке ![]() непрерывна, а значит, интегрируема, то предел интегральной суммы не зависит от разбиения и выбора точек:
непрерывна, а значит, интегрируема, то предел интегральной суммы не зависит от разбиения и выбора точек:

Б) В этом случае выражение под знаком предела представляет интегральную сумму для функции 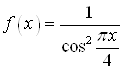 на промежутке
на промежутке ![]() , соответствующую разбиению отрезка на равные части, точки
, соответствующую разбиению отрезка на равные части, точки ![]() выбраны на левых концах промежутков:
выбраны на левых концах промежутков: ![]() .
.
Поскольку 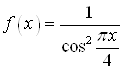 интегрируема на
интегрируема на ![]()

Пример 3. Вычислить среднее значение функции ![]() на промежутке
на промежутке ![]() .
.
Решение: по определению среднее значение ![]() на
на ![]() равно
равно
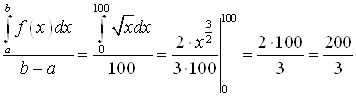 .
.
| < Предыдущая | Следующая > |
|---|