01. Интеграл Римана. Основные определения
1. Разбиением Р отрезка ![]() называется конечная система точек
называется конечная система точек ![]() Отрезки
Отрезки ![]() называются отрезками разбиения. Диаметром разбиения
называются отрезками разбиения. Диаметром разбиения ![]() называется максимум длин отрезков разбиения:
называется максимум длин отрезков разбиения:
2. Если на каждом из отрезков ![]() , соответствующих разбиению Р выбрана точка
, соответствующих разбиению Р выбрана точка ![]() , то определено разбиение Р с выбором точек
, то определено разбиение Р с выбором точек ![]() .
.
3. Пусть на ![]() задана функция
задана функция ![]() , Р – разбиение
, Р – разбиение ![]() ,
, ![]() - выбор точек.
- выбор точек.
Сумма 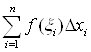 называется Интегральной Суммой для
называется Интегральной Суммой для ![]() на
на ![]() , соответствующей данному разбиению Р и данному выбору точек
, соответствующей данному разбиению Р и данному выбору точек ![]() :
:
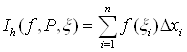 .
.
4. Если существует предел ![]() когда диаметр разбиения
когда диаметр разбиения ![]()
![]() и этот предел не зависит от разбиения Р и выбора точек
и этот предел не зависит от разбиения Р и выбора точек ![]() , то он называется Римана от функции
, то он называется Римана от функции ![]() на промежутке
на промежутке ![]() и обозначается
и обозначается ![]() .
.
5. Функция ![]() , для которой
, для которой ![]() называется интегрируемой на
называется интегрируемой на ![]() по Риману или просто интегрируемой,
по Риману или просто интегрируемой, ![]() и
и ![]() называются соответственно верхним и нижним пределами интегрирования,
называются соответственно верхним и нижним пределами интегрирования, ![]() - переменной интегрирования.
- переменной интегрирования.
6. Теорема (Необходимый признак интегрирования)
Если функция ![]() интегрируема на
интегрируема на ![]() , то она ограничена на этом промежутке.
, то она ограничена на этом промежутке.
Ограниченность не является достаточным признаком: существует ограниченные на ![]() функции не являющиеся интегрируемыми. Примером таких функций является функция Дирихле:
функции не являющиеся интегрируемыми. Примером таких функций является функция Дирихле:
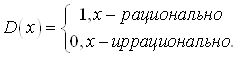
7. Нижней интегральной суммой Дарбу функции ![]() , соответствующей разбиению Р называется
, соответствующей разбиению Р называется
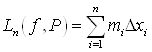
![]()
8. Верхней интегральной суммой Дарбу, соответствующей разбиению Р, называется
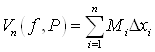
![]()
Суммы Дарбу обладают следующими свойствами:
1) Интегральная сумма, соответствующая данному разбиению и данному выбору точек ![]() удовлетворяет неравенствам
удовлетворяет неравенствам
![]() .
.
2) При увеличении количества точек разбиения нижняя интегральная сумма разве что увеличивается, а верхняя – разве что уменьшается.
3) Каковы бы ни были разбиения ![]()
![]() .
.
4) Множество всех нижних интегральных сумм ![]() ограничено сверху, множество всех верхних интегральных сумм
ограничено сверху, множество всех верхних интегральных сумм ![]() - снизу.
- снизу.
5) Infimum множества ![]() называется верхним интегралом и обозначается
называется верхним интегралом и обозначается 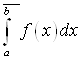 .
.
6) Supremum множества ![]() - нижним интегралом и обозначается
- нижним интегралом и обозначается 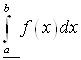 .
.
| Следующая > |
|---|