04. Нормальный алгорифм Маркова

Прежде всего необходимо заметить, что в нашем курсе (и, соответственно, в этой статье) нормальный алгорифм рассматривается исключительно как точная модель алгоритма, но не как основа дальнейшего построения математики в рамках конструктивного направления [8]. Можно сказать, что мы строим некоторую теоретико-множественную модель нормального алгорифма, определяя это понятие аналогично похожим понятиям в теории формальных языков (например, понятиям грамматики или автомата [9]).

Начнем с некоторых предварительных определений.

Пусть некоторый алфавит, а и слова в этом алфавите.

Говорят, что Слово входит в слово , если существуют такие слова (возможно пустые), что . Например, слова «ход» и «вход» входят в слово «входит». Соответствующее отношение на множестве слов будем обозначать , используя тем самым запись . Очевидны следующие свойства этого отношения: каждое слово входит само в себя (отношение рефлексивно), пустое слово (обозначаемое далее буквой ) входит в любое слово, и если , а , то . Тем самым отношение Является предпорядком.

Если , то возникает упорядоченная тройка слов , называемая Вхождением слова в слово . В теории нормальных алгорифмов вхождение записывают так: , где «звездочка» является «метасимволом», не принадлежащем алфавиту . При этом пустое слово часто не пишется вообще, то есть, например, вхождение слова «вход» в слово «входит» следует записывать так: *вход*ит. Слово называют Левым, а слово Правым Крылом вхождения.

Одно и то же слово может входить в другое слово несколько раз. Например, . Мы имеем тут два вхождения: И . Среди всех вхождений слова В слово Выделяют первое, или главное. Это то, которое имеет наименьшую длину левого крыла, то есть самое левое. Из показанных выше двух вхождений первое как раз будет главным.

Дадим теперь определение формулы подстановки.

Формула подстановки в алфавите есть, по определению, упорядоченная пара слов в этом алфавите, записываемая в виде , где «стрелка» есть опять-таки метасимвол, отделяющий Левую часть формулы (слово ) от Правой (слова ). Часто дальше будем говорить просто «формула» вместо «формула подстановки».

Пусть теперь есть формула , а . Говорят, что Формула применима к слову (или является Подходящей для слова ), если ее левая часть входит в слово: . Пусть - первое вхождение в . Результат Применения формулы к слову есть слово . Это схематически можно показать так:

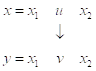
Говорят в этом случае, что СловоПолучено в результате замены первого вхождения левой части формулы в слово на правую.

Такую операцию над исходным словом называют также Нормальной подстановкой.

Основное определение: Нормальный алгорифм (НА) в алфавите есть упорядоченная тройка , где - Схема НА, представляющая собой упорядоченный набор (кортеж, конечная последовательность) формул подстановки в алфавите , в котором отмечены некоторые формулы, называемые Заключительными и образующие частичный кортеж (подпоследовательность) . Заключительная формула в схеме отмечается точкой после стрелки.

Будем далее, если контекст это позволяет, пользоваться аббревиатурой НА, или говорить просто «алгорифм», имея в виду именно нормальный алгорифм Маркова.

Пример схемы:

(5)

Здесь предполагается, что это схема НА в алфавите , причем третья сверху формула является заключительной, а левая часть самой нижней формулы есть пустое слово.

Из приведенного примера можно понять синтаксис записи схем нормальных алгорифмов: формулы схемы пишутся в столбик и упорядочиваются сверху вниз, схема окаймляется левой фигурной скобкой и предваряется обозначением НА с двоеточием.

В общем случае схема НА выглядит так:

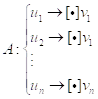
Квадратные скобки означают необязательность вхождения точки.

Так строится «статическая» часть определения нормального алгорифма. Теперь нужно определить «динамику», то есть точно определить процесс преобразования слов, задаваемый нормальным алгорифмом. Есть смысл сначала дать содержательное описание этого процесса, называемого Процессом работы НА с исходным словом.

Пусть задан НА и входное слово (в каком-то алфавите).

Схема НА просматривается сверху вниз в поисках первой применимой ко входному слову формулы. Если таковой не оказывается, то процесс заканчивается и само входное слово считается его результатом (то есть НА вычисляет тогда тождественную функцию). Иначе, найденная формула применяется, как описано выше (операция нормальной подстановки). Если эта формула оказалась простой (не заключительной), то с полученным в результате ее применения словом поступают так же, как с исходным. Если же она оказалась заключительной, то после ее применения процесс заканчивается и слово, полученное в результате ее применения, считается результатом. Таким образом, процесс продолжается до тех пор, пока не произойдет одно из двух событий: 1) Естественный обрыв, когда в схеме нет ни одной применимой к текущему слову формулы; в этом случае говорят, что слово не поддается данному НА (или его схеме), и оно считается результатом; 2) к текущему слову была применена заключительная формула, и тогда результатом считается слово, полученное применением этой формулы к текущему. Может оказаться, что ни одном из шагов не выполняется условие останова (прекращения процесса). В этом случае результат не определен, и говорят, что данный НА не применим ко входному слову.

Чтобы дать точное (формальное) определение процесса работы, нужно ввести некоторые обозначения и определения.

1) Будем писать и говорить, что НА непосредственно просто переводит слово в слово , если , где - первая (самая верхняя) формула в схеме НА, оказавшаяся простой.

2) Будем писать и говорить, что НА непосредственно заключительно переводит слово в слово , если , где - первая (самая верхняя) формула в схеме НА, оказавшаяся заключительной.

3) Будем писать И говорить, что НА просто переводит слово в слово (без слова «непосредственно»!), если существует последовательность слов в которой для каждого выполняется .

4) Будем писать и говорить, что НА заключительно переводит слово в слово , если или существует такое слово , что И .

Можно сказать, что в пп. (1) и (2) дано формальное определение Шага процесса работы НА со словом, а в пп. (3) и (4) определяется последовательность таких шагов (в том числе и один шаг).

5) Будем писать , когда слово Не поддается НА .

Теперь мы можем дать строгое определение процесса работы НА со словом.

Процесс работы НА со словом есть конечная или бесконечная последовательность слов Где , причем для каждого или , если слово определено в последовательности. Это слово, как и все последующие, считается не определенным, если , то есть последнее слово получено применением заключительной формулы, или , то есть последнее слово не поддается НА и имеет место естественный обрыв процесса работы.

Если процесс работы НА со словом конечен, то его последнее слово обозначается и называется Результатом работы НА со словом . В этом случае говорят, что НА применим к слову И пишут . В противном случае говорят, что НА не применим к слову и пишут .

Чтобы завершить описание основной модели алгоритма (НА), необходимо определить понятие вербальной функции, вычислимой по Маркову и сформулировать основную гипотезу, утверждающую универсальность предложенной модели.

Вербальная функция Типа Называется Вычислимой по Маркову, если может быть построен НА такой, что для любого слова имеет место следующее: тогда и только тогда, когда , и в этом случае .

Необходимо обратить внимание, что в этом определении вместо слова «существует» (в определении интуитивной вычислимости) стоит «можно построить». Это очень важно: чтобы доказать вычислимость по Маркову, нужно предъявить схему соответствующего НА и доказать, что этот НА вычисляет заданную функцию, то есть доказательство должно быть конструктивным. Конечно, в любом случае, при разработке алгоритма необходимо его точное описание и доказательство корректности, но всё равно тогда возникает некое уточнение интуитивного понимания алгоритма, например, в виде псевдокода или даже программы на языке высокого уровня. То есть всякий раз, когда от интуитивной концепции вычислимости мы переходим к той или иной точной модели, доказательство вычислимости функции обязано быть конструктивным. Это, повторим, важнейший аспект в методике преподавания теории алгоритмов студентам-программистам.

Основная гипотеза теории алгоритмов в версии теории нормальных алгорифмов Маркова называется Принципом нормализации и состоит в следующем:

Всякая вербальная функция, вычислимая в интуитивном смысле слова, вычислима по Маркову.

Подчеркнем, что это именно гипотеза, а не теорема, так как в формулировке фигурирует не определенное математически точно понятие функции, вычислимой в интуитивном смысле слова.

На этом описание основной модели закончено.

Рассмотрим некоторые примеры нормальных алгорифмов, важные для дальнейшего изложения.

Примеры

1) Тождественный НА , задаваемый схемой

Любое слово в заданном алфавите перерабатывает в это же слово за один шаг, то есть

.

2) Нигде не применимый НА , задаваемый схемой

Очевидно, что для любого входного слова процесс работы такого НА с ним будет бесконечным, то есть

3) НА левого присоединения фиксированного слова.

НА , заданный схемой

,

Где - фиксированное слово в алфавите , вычисляет функцию левого присоединения к любому слову в алфавите данного слова , то есть

4) НА правого присоединения фиксированного слова.

НА , заданный схемой

(6)

В алфавите , где , вычисляет функцию правого присоединения данного фиксированного слова в алфавите К любому слову в алфавите , т. е.

Действительно, к произвольному слову применима только самая нижняя формула в схеме алгорифма . После ее применения оказывается применимой одна из формул верхней строки, если слово не пусто. Эти формулы применяются до тех пор, пока «решетка» (#) не окажется последней буквой очередного слова, выводимого из исходного слова . Тогда она посредством применения средней формулы схемы заключительно заменяется на слово .

Заметим, что в этой схеме фигурирует параметр , пробегающий алфавит , и, тем самым, верхняя строка схемы представляет конечное множество формул, число которых равно числу букв алфавита . В схему НА можно вводить параметры, но необходимо, чтобы он пробегал некоторое конечное множество. Схема НА , как нетрудно видеть, обобщает схему (5).

5) НА удвоения

Рассмотрим НА Double, задаваемый схемой в алфавите V1 = VÈ{a, b}, причем a, b Ï V:

(7)

Можно показать, что , т. е. этот алгорифм удваивает любое входное слово в алфавите V.

Мы в рамках этой работы, ради экономии объема, не анализируем подробно работу приведенных в примерах нормальных алгорифмов. Подробности такого рода будут рассмотрены в отдельной публикации, специально посвященной проблемам технике разработки схем нормальных алгорифмов.

Можно заметить также, что если вместо формулы поставить формулу , то копия будет инвертирована, т. е. получится слово .

Если схему (7) модифицировать следующим образом

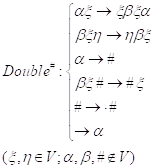(8)

То получим алгорифм удвоения через разделитель, то есть .

< Предыдущая		Следующая >