13. Интегрирование иррациональных выражений
1°. Интегралы вида  заменой переменной
заменой переменной ![]() приводятся к интегралу от рациональной функции, а значит, интегрируются в элементарных функциях.
приводятся к интегралу от рациональной функции, а значит, интегрируются в элементарных функциях.
2°. Интегралы вида
 ,
,
Где ![]() – целые числа приводятся к интегралу от рациональной функции заменой
– целые числа приводятся к интегралу от рациональной функции заменой ![]() , где
, где ![]() – общий знаменатель дробей
– общий знаменатель дробей 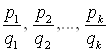 , и интегрируются в элементарных функциях.
, и интегрируются в элементарных функциях.
3°. Интегралы вида
|
1) |
|
2) |
|
3) |
Приводятся к ![]() с помощью тригонометрической замены
с помощью тригонометрической замены
|
1) |
|
Где |
|
2) |
|
Где |
|
3) |
|
Где |
Интегралы всех перечисленных выше видов вычисляются в элементарных функциях.
4°. Дифференциальным биномом называют выражение вида ![]() , где
, где ![]() – вещественные числа,
– вещественные числа, ![]() – рациональные числа.
– рациональные числа.
Теорема Чебышева утверждает, что дифференциальный бином интегрируется в элементарных функциях только в трех случаях:
|
1) |
|
|
|
2) |
|
|
|
3) |
|
|
Примеры. Вычислить неопределенные интегралы:
|
1) |
2) |
|
3) |
4) |
|
1) |
|
|
| |
|
| |
|
2) |
|
|
| |
|
| |
|
3) |
|
|
| |
|
4) |
|
|
| |
|
| |
|
| |
|
|
Интегралы вида 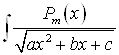 , где
, где ![]() - многочлен степени, большей, чем 1, вычисляются по следующей формуле
- многочлен степени, большей, чем 1, вычисляются по следующей формуле
 (*)
(*)
Здесь ![]() - число,
- число, ![]() - многочлен, степени на единицу меньшей, чем
- многочлен, степени на единицу меньшей, чем ![]() . Все коэффициенты находятся методом неопределенных коэффициентов.
. Все коэффициенты находятся методом неопределенных коэффициентов.
Для этого следует продифференцировать равенство (*), преобразовать и сравнить коэффициенты при одинаковых степенях ![]() . Покажем процедуру вычисления неопределенных коэффициентов на примере.
. Покажем процедуру вычисления неопределенных коэффициентов на примере.
Пример: Вычислить интеграл

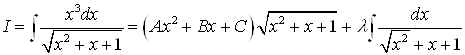
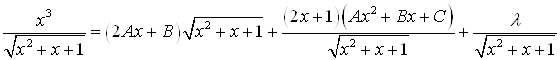


Таким образом,

Интегралы вида  приводятся к предыдущему подстановкой
приводятся к предыдущему подстановкой ![]() .
.
Пример. Вычислить

Решение.

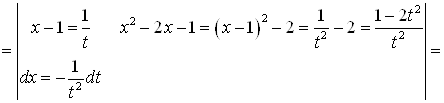

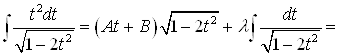
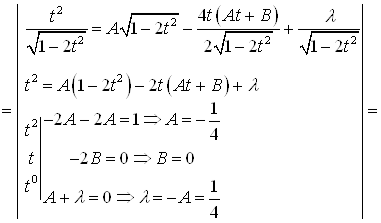

 .
.
| < Предыдущая | Следующая > |
|---|
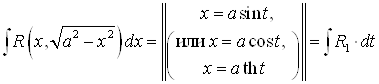 ,
,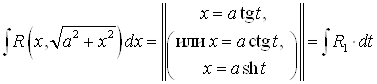 ,
, ,
,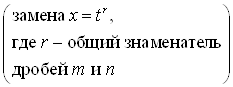 ;
; ;
;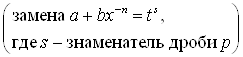 .
. ;
; ;
; ;
; .
.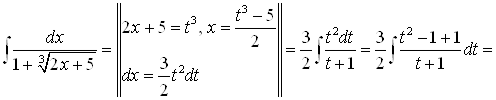
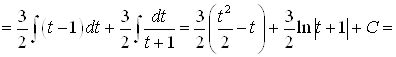
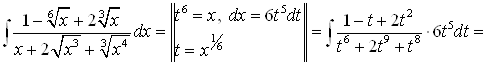

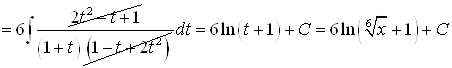 ;
;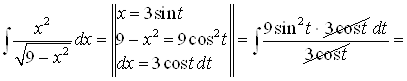




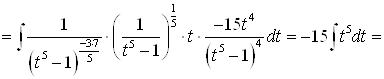
 .
.